L'AMPLIFICATORE OPERAZIONALE
Se dovessimo costruire un amplificatore per grandezze continue esso dovrà presentare i seguenti requisiti:
Non analizzeremo nel dettaglio le specifiche sopra riportate, in quanto ciò è già stato fatto, in modo sufficientemente approfondito, nel capitolo precedente.
Tutte queste caratteristiche, una volta rispettate, fanno sì che l'amplificatore che le realizzi venga definito AMPLIFICATORE OPERAZIONALE.
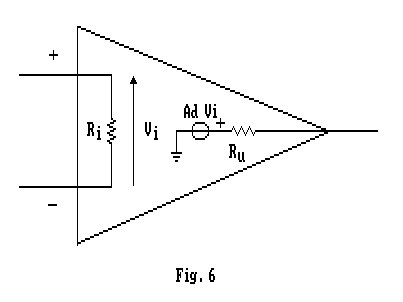
Esistono molte tecniche per poterlo realizzare; ad esempio utilizzando transistor a giunzione, oppure transistor ad effetto di campo, od ancora tecniche di campionamento. Risulta comunque scomodo analizzare il suo funzionamento, una volta inserito in un circuito, disegnandone lo schema effettivo; pensiamo, pertanto, di realizzarci un modello che sia equivalente all'amplificatore operazionale per gli effetti esterni, ma che presenti una complessità circuitale inferiore. Inoltre, il circuito equivalente sarà valido per qualsiasi tipo di amplificatore ed i suoi parametri saranno ricavabili, direttamente, da misure esterne effettuate sullo stesso. Il simbolo rappresentato in Fig. 1 sarà, d'ora in poi, utilizzato per indicare l'amplificatore operazionale.
Si noti che il segno "+" indica l'ingresso non invertente nei confronti dell'uscita, mentre il segno "-" indica l'ingresso invertente.
Vogliamo, ora, ricavare il circuito equivalente valido per le sole variazioni del segnale, cioè indipendentemente dai livelli continui. Supponiamo, inoltre, che le variazioni assumano valori tali per cui l'operazionale lavori in zona lineare; è, così, possibile utilizzare il principio di sovrapposizione degli effetti e studiare sul componente, separatamente, gli effetti dell'applicazione di una tensione di modo comune vc e di una tensione di modo differenziale vd.
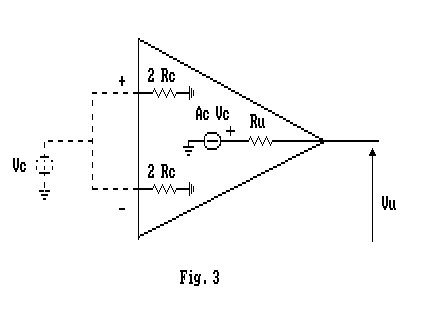
Allo scopo utilizziamo il circuito di Fig. 2: troveremo che per ogni valore della tensione d'ingresso vc l'uscita sarà ad essa proporzionale. Potremo, così, scrivere che Vu = Ac vc , in cui con Ac è intesa l'amplificazione di modo comune.
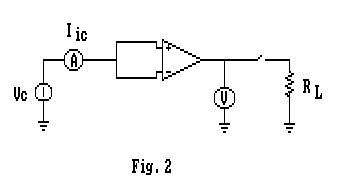
Da questo circuito ricaviamo, inoltre, la corrente d'ingresso iic proporzionale a vc, cioè possiamo scrivere:
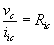
da cui possiamo definire la Ric come impedenza d'ingresso per il modo comune. Il valore di tale impedenza è sempre molto alto, da 100 a 1000 , per amplificatori che utilizzano transistor bipolari, e raggiunge 1012 per amplificatori impieganti FET.
Se inseriamo il carico RL ci accorgiamo che l'uscita vu diminuisce lievemente, questo per effetto di una resistenza d'uscita dell'amplificatore Ru non nulla che, facendo partizione col carico, può essere facilmente ricavata dalla formula:
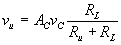
Le misure effettuate ci consentono di tracciare un primo circuito equivalente valido per il modo comune:
Ora utilizziamo il circuito di Fig.4, dove all'ingresso dell'amplificatore è stato posto un segnale differenziale bilanciato rispetto a massa.
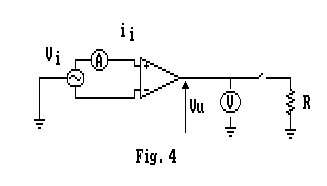
All'uscita, a vuoto, misuriamo una tensione vu proporzionale a vi, pari a ![]() dove Ad è l'amplificazione differenziale. In ingresso valutiamo una variazione di corrente ii proporzionale alla tensione applicata, che possiamo considerare dovuta ad una resistenza differenziale Rid.
dove Ad è l'amplificazione differenziale. In ingresso valutiamo una variazione di corrente ii proporzionale alla tensione applicata, che possiamo considerare dovuta ad una resistenza differenziale Rid.
Ancora una volta caricando l'uscita possiamo ricavare la resistenza Ru che è, comunque, uguale a quella ricavata in precedenza dato che lo stadio finale è, chiaramente, unico.
Da queste considerazioni ed applicando il principio di sovrapposizione degli effetti, ricaviamo il circuito equivalente di Fig.5.
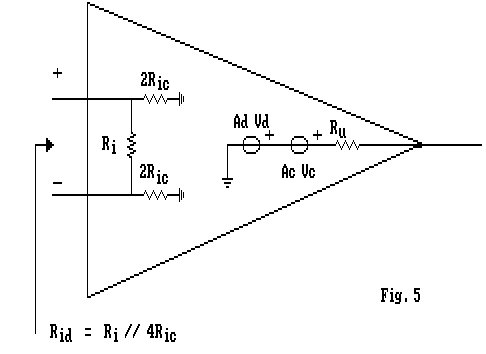
La resistenza d'ingresso sarà:
![]()
Se , Ric >> Ri allora ![]() . Questo in generale è vero per gli amplificatori con stadio d'ingresso a transistor, mentre per gli amplificatori con ingresso a FET le resistenze Ric e Ri risultano dello stesso ordine di grandezza, quindi per questi operazionali non possiamo applicare la semplificazione proposta qui di seguito.
. Questo in generale è vero per gli amplificatori con stadio d'ingresso a transistor, mentre per gli amplificatori con ingresso a FET le resistenze Ric e Ri risultano dello stesso ordine di grandezza, quindi per questi operazionali non possiamo applicare la semplificazione proposta qui di seguito.
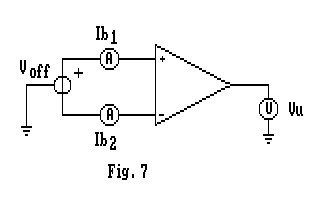
Vediamo, ora, cosa succede inserendo un segnale bilanciato Voff tale che, con resistenze nulle sugli ingressi, mi fornisca .
Come già visto nei capitoli precedenti Voff, tensione differenziale di ingresso che riporta al valore nominale (0 V) la tensione di uscita, viene denominata TENSIONE di OFFSET ALL'INGRESSO. In queste condizioni nei due ingressi scorrono le correnti Ib1 e Ib2.
la corrente di polarizzazione d'ingresso (INPUT BIAS CURRENT )
la corrente di offset in ingresso. (INPUT OFFSET CURRENT )
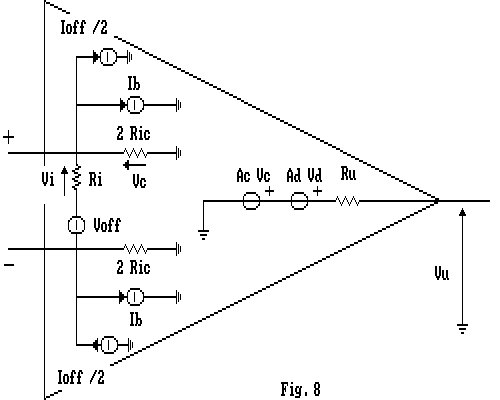
Possiamo così applicare un'ultima volta il principio di sovrapposizione degli effetti costruendoci il circuito equivalente completo dell'amplificatore operazionale.
GLI AMPLIFICATORI OPERAZIONALI
E
LA REAZIONE NEGATIVA
Un amplificatore operazionale, presentando guadagno di tensione elevatissimo, sarà utilizzato praticamente solo in modo reazionato e, con queste caratteristiche, la funzione di trasferimento può essere resa effettivamente dipendente dai soli elementi costituenti l'anello di reazione. Di questi circuiti ci interessa, normalmente, conoscere il guadagno, la resistenza d'ingresso e quella d'uscita.
Per calcolare in modo esatto queste grandezze, dovremmo sostituire all'operazionale il suo circuito equivalente completo (fig.8) e risolvere la rete costituita da questo e dal circuito di reazione. Altrimenti potremmo decidere di valutare in modo approssimato il comportamento del circuito. Per far ciò assumiamo che ![]() e (fig.9).
e (fig.9).
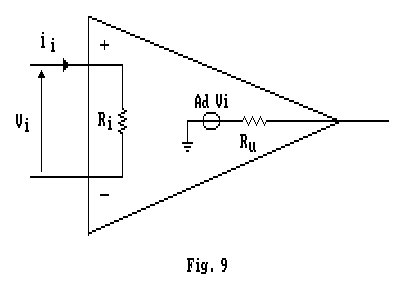
Allora si avrà:
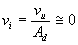 e
e 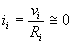
Si noti che tali approssimazioni sono valide solo per il funzionamento in zona lineare, in quanto, al di fuori di essa, non è più possibile trovare un fattore di proporzionalità fra Vi e Vu né è lecito considerare![]() .
.
Queste approssimazioni sono molto usate sia in sede di progettazione che di analisi dei circuiti e, solo se necessario, si procederà ad un calcolo più rigoroso.
AMPLIFICATORE DI TENSIONE NON INVERTENTE
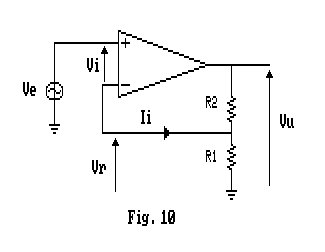
L'amplificatore di tensione non invertente ha la configurazione circuitale mostrata in Fig.10. Come si può notare, prelevo una tensione in uscita, riportandola, come tensione, in serie alla maglia d'ingresso. La reazione sarà quindi di tensione- serie, ovvero, parallelo - serie.
Nell'ipotesi che la Ri dell'amplificatore operazionale sia infinita, possiamo facilmente calcolare la tensione Vr che può essere valutata tramite il calcolo del partitore di tensione su R1, essendo nulla la corrente Ii,
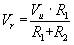
Considerando, però, nulla la Vi, avremo che Vr
º Ve. Sostituendo opportunamente e ricavando il rapporto delle tensioni si ottiene:![]() da cui abbiamo
da cui abbiamo ![]()
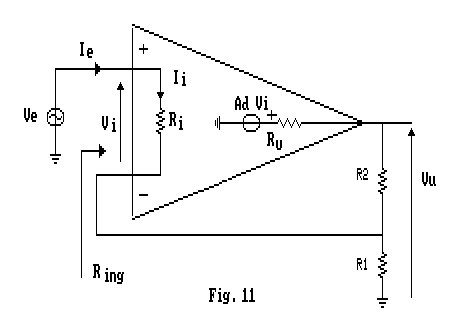
Dobbiamo calcolare ora la resistenza di ingresso del circuito, ricorriamo quindi al seguente schema trascurando, in prima approssimazione, la resistenza d'ingresso per il modo comune.
La resistenza che si vede dai morsetti d'ingresso sarà:
![]() ma
ma ![]()
Essendo ![]() , possiamo dire che:
, possiamo dire che: ![]()
![]()
sostituendo, otteniamo: ![]() , riscrivendola
, riscrivendola
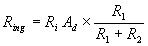
In conclusione la resistenza di ingresso è, generalmente, molto elevata, quindi non è sempre lecito trascurare l'influenza dell'impedenza d'ingresso per il modo comune.
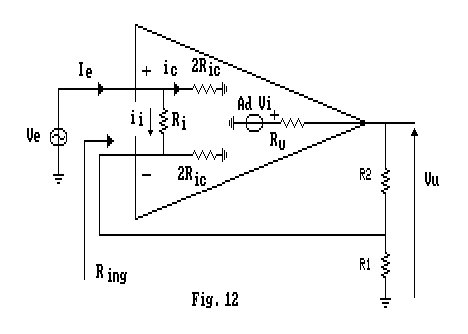
A tal scopo consideriamo il circuito di Fig.12, abbiamo che:
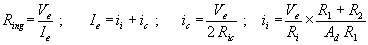
allora:
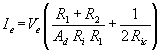
da cui:
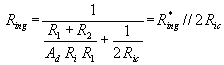
in cui R*ing è la resistenza di ingresso calcolata trascurando la Ric, come visto in precedenza.
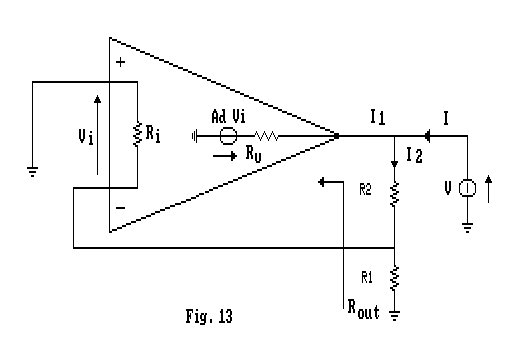
La resistenza d'uscita può essere ricavata dal circuito seguente, come la resistenza che si vede dai morsetti del carico, con segnale d'ingresso nullo.
![]() ma
ma ![]()
dove, considerando Ri >> R1, possiamo scrivere:
![]() ed
ed ![]()
(se l'ipotesi non fosse verificata dovremmo sostituire a R1 il parallelo fra Ri e R1 stessa), ma
![]()
da cui:
![]()
Poiché Ad è molto elevata si verifica che I2 << I1 quindi possiamo concludere che:
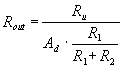
Da questa relazione si può concludere che l'impedenza d'uscita è estremamente bassa.
L'amplificatore di tensione non invertente presenta, quindi, un'elevata impedenza d'ingresso ed una bassissima impedenza d'uscita, la qual cosa lo rende estremamente adattato come amplificatore di tensione d'elezione, essendo pressocchè immune da effetti di partizione.
AMPLIFICATORE DI TRANSRESISTENZA
Si preleva una tensione in uscita e la si riporta, come corrente, in parallelo alla maglia d'ingresso, quindi sarà una reazione di tensione - parallelo, ovvero, parallelo - parallelo.
La funzione di trasferimento sarà data da:
![]()
Bisogna notare che la tensione di uscita risulta "pilotata" dalla corrente in ingresso, questo giustifica il nome di amplificatore di transresistenza, dato al circuito.
Dall'equazione al nodo B, risulta:
![]()
ma, non entrando corrente nell'operazionale, Ii = 0. Ne deriva, quindi, che Ie=Ir. Inoltre Vi = 0, ciò implica che il punto B sia praticamente a potenziale di massa. Infatti, si suole indicare B come "Massa Virtuale", ovvero B risulta una massa per le tensioni, ma non per la correnti.
Per le posizioni espresse in precedenza sarà ![]() ed essendo
ed essendo ![]() posso dire che
posso dire che ![]() ovvero
ovvero ![]()
Calcoliamo, ora, la resistenza di ingresso del circuito riferendoci alla Fig.15.
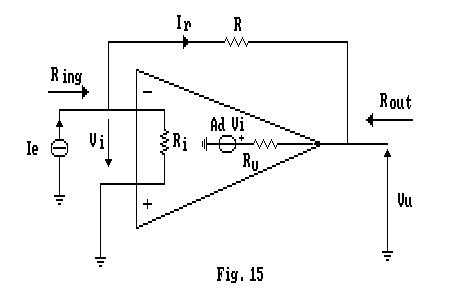
![]() quindi
quindi ![]()
Come si vede, la resistenza di ingresso per questa configurazione è molto bassa.
Per il calcolo della resistenza d'uscita, consideriamo l'espressione ottenuta dall'analisi del circuito di Fig.13:
prendendo il limite per ![]() , otteniamo
, otteniamo ![]() , che è ancora un valore estremamente basso.
, che è ancora un valore estremamente basso.
In conclusione, l'amplificatore di transresistenza presenta una tensione d'uscita direttamente proporzionale alla corrente d'ingresso e resistenze d'ingresso e d'uscita bassissime.
Dall'amplificatore di transresistenza, deriva direttamente l'amplificatore di tensione invertente:
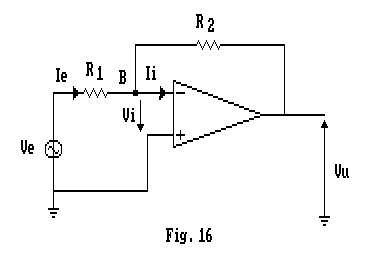
Anche di questo circuito calcoleremo il guadagno, procedendo come segue.
Considerando che, essendo Vi = 0, e che, pertanto, il punto B è una massa virtuale, la resistenza che si vedrà fra B e massa è nulla, ovvero, la conduttanza parallela di Norton è infinita. Sotto queste ipotesi, sostituendo al ramo serie l'equivalente di Norton visto fra la massa ed il morsetto B, otteniamo il circuito di Fig. 17, in cui ![]() .
.
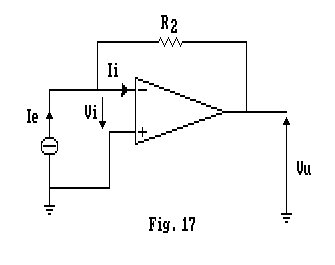
Tale circuito è formalmente uguale a quello riportato nella Fig. 14.
Sostituendo nella espressione, ad esso relativa, vista poc'anzi, ![]() , il valore di Ie ottenuto, ed al posto di R, R2, avremo:
, il valore di Ie ottenuto, ed al posto di R, R2, avremo:
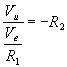
dalla quale si ottiene:
![]()
Per il calcolo della resistenza d'ingresso riferiamoci, ancora, al circuito di Fig.16 notiamo che:
![]()
ma, essendo ![]() , è lecito scrivere che:
, è lecito scrivere che:
![]() e, siccome Ad è molto grande, vediamo che
e, siccome Ad è molto grande, vediamo che ![]() , da quanto detto deriva che:
, da quanto detto deriva che: ![]() .
.
Per quanto riguarda la resistenza d'uscita è facile dimostrare, come si è già fatto per l'amplificatore di tensione non invertente, che Rout è molto bassa, infatti essa è ancora data dalla relazione seguente:
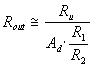
AMPLIFICATORE DI TRANSCONDUTTANZA
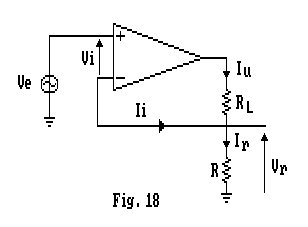
Si preleva una corrente in uscita riportandola come tensione in ingresso, sarà quindi una reazione di corrente serie, ovvero serie - serie.
Nell'ipotesi che Vi = 0, avremo Ve = Vr = R·Ir.
Inoltre, essendo sempre Ii = 0 e considerando che Ir = Ii + Iu, si otterrà Ir = Iu che, tramite opportune sostituzioni ci fornisce la relazione:
![]()
Questo amplificatore fornisce ad un carico Rl, una corrente direttamente proporzionale alla tensione pilota Ve, questo giustifica il nome di amplificatore di transconduttanza. Il suo grosso inconveniente, è costituito dal fatto, che, non possedendo il carico alcun capo a massa e, quindi, non essendo connesso ad alcun potenziale di riferimento, rimane fluttuante.
Il calcolo della resistenza d'ingresso di questo circuito, può essere condotto osservando che esso è topologicamente identico all’amplificatore di tensione non invertente.
Per comodità riportiamo il circuito utilizzato per il computo, dal quale si ricava:
![]()
Come si nota, per l'elevato valore di Ad, anch'essa avrà un valore molto alto.
Per quanto concerne la resistenza d'uscita, consideriamo il circuito di Fig.19:
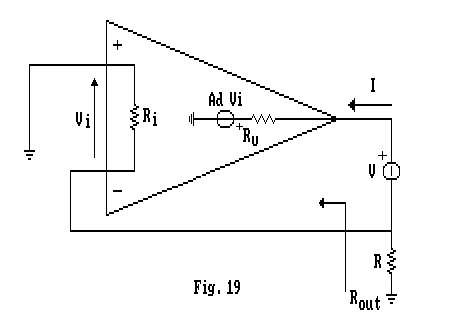
Per chiarezza, è bene ridisegnarlo come segue:
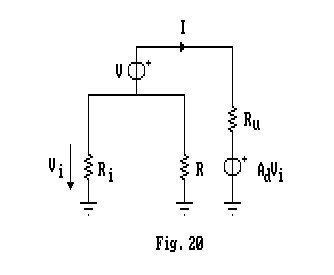
Risolvendo il circuito, otteniamo:
![]()

ma, ![]() da cui:
da cui: ![]()
allora:
![]()
Da cui
![]()
Valore che risulta estremamente elevato.
AMPLIFICATORE DI CORRENTE
Si preleva una corrente in uscita e la si riporta come corrente in ingresso. Pertanto avremo una reazione di corrente-parallelo, ovvero serie-parallelo.
Ipotizzando Vi = 0, si ottiene che la corrente Iu si ripartisce nelle due resistenze R1 ed R2. Risolvendo il partitore di corrente, troviamo che
![]()
Dall'ipotesi che Ii= 0, risulta Ir = - Ie, pertanto
![]()
Anche questo amplificatore ha l'inconveniente di richiedere un carico fluttuante, cioè senza alcun capo a massa.
Volendo calcolare, anche per questo circuito, le resistenze d'ingresso e d'uscita, si può ricorrere a ragionamenti già visti in precedenza ottenendo così, che la resistenza d'ingresso è molto bassa mentre quella d'uscita risulta estremamente elevata.
"VOLTAGE FOLLOWER"
L’inseguitore di tensione, deriva direttamente dall’amplificatore di tensione non invertente, quando si faccia tendere R2 a zero ed R1 all’infinito (vedi Fig.11). Il circuito risultante è quello che segue:
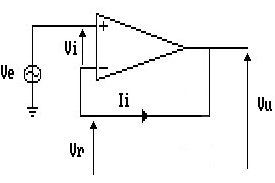
Considerando che la Vi è praticamente uguale a 0, otteniamo che ![]() .
.
Presenterà, quindi, amplificazione di tensione estremamente prossima ad 1, unitamente ad un’altissima impedenza di ingresso (circa pari a 2·Ric) ed ad una bassissima impedenza di uscita. Pertanto, essendo privo da rapporti di partizione, sarà utilizzato come adattatore di impedenza fra una sorgente ad alta impedenza di uscita ed un utilizzatore di bassa impedenza.