ad uso del I e II segmento POLIS
nei corsi di Scienze Applicate
e di Elettrotecnica ed Elettronica
1
L'Algebra di Boole
L'algebra di Boole (1815 - 1864) è un insieme di elementi che possono assumere solo due valori, o
stati, distinti e contrari che, convenzionalmente, vengono indicati dai simboli
0 ed
1.
Gli elementi, o
variabili, booleani possono essere legati dagli operatori di somma (+) e prodotto (
).
Per ogni coppia delle variabili x ed y appartenenti ad un insieme booleano, anche operazioni fra di essi generano variabili booleane.
Fra gli elementi dell'insieme booleano esistono delle relazioni fondamentali dette
postulati e delle proprietà fondamentali.
1.1
Postulati dell'algebra booleana
-
Se allora ovvero se allora
-
ovvero In questo postulato compaiono due formule che possono essere ricavate l'una dall'altra sostituendo 0 con 1 e + con . Questa proprietà è detta “dualità”
-
-
-
1.2
Leggi fondamentali
la doppia negazione afferma
1.3
Alcuni Teoremi dell'Algebra di Boole
oppure
oppure
Facilmente dimostrabile applicando il principio di dualità.
2
Funzioni Booleane e Tavole della Verità
Le funzioni booleane stabiliscono delle relazioni fra variabili booleane esprimibili mediante espressioni algebriche in cui le stesse vengono legate per mezzo di operatori fondamentali (somma, prodotto e negazione).
Ogni funzione booleana può venir rappresentata tramite l'espressione implicita
che assumerà un valore logico
0 o
1 in relazione ai valori logici assunti dalle variabili.
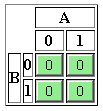
Per rappresentare in forma sintetica tutti i valori logici che una funzione può assumere, si usa normalmente la tavola della verità della funzione stessa.
La tavola (o tabella
) della verità contiene tutte le possibili combinazioni delle variabili dalle quali questa dipende con i corrispondenti stati della funzione.
Supponiamo, ad esempio, di avere la seguente funzione:
la corrispondente tabella della verità sarà:
2.1
Le Forme Canoniche
Le funzioni booleane possono essere rappresentate secondo un formato standard costituito o da una somma di prodotti delle variabili o da un prodotto di somme.
Si definisce
forma canonica di una funzione booleana ogni rappresentazione esplicita che contenga, in forma diretta o inversa, tutte le variabili in ogni termine.
Se la forma canonica contiene termini canonici costituiti da prodotti delle variabili la funzione si dice sia rappresentata per “
minterm”, viceversa se è rappresentata da somme delle variabili si dirà che è rappresentata da “
maxterm”.
Ad esempio, la funzione
è una forma canonica composta da
somme di minterm, mentre la funzione
è una forma canonica composta da
prodotti di maxterm. La funzione
non è una forma canonica in quanto contiene sia minterm che maxterm e l'ultimo termine non contiene tutte le variabili.
Il numero massimo di minterm o di maxterm è dato dal numero di possibili combinazioni delle variabili quindi, con
n variabili, avremo
minterm o maxterm.
Ogni minterm può essere espresso anche mediante un numero decimale equi-valente alla combinazione binaria che si ottiene sostituendo
1 alle variabili che compaiono in forma diretta e
0 a quelle che compaiono in forma negata, dopo averle ordinate secondo un criterio prestabilito.
In modo analogo, ogni maxterm può essere rappresentato anche mediante un numero decimale equivalente alla combinazione binaria che si ottiene sostituendo
1 alle variabili che compaiono in forma negata e
0 a quelle che compaiono in forma diretta.
Ad esempio
e
.
può essere rappresentata con l'espressione:
In modo del tutto analogo, la funzione:
può essere rappresentata con l'espressione:
Nella seguente tabella riportiamo tutti i minterm ed i maxterm che possono essere contenuti in una funzione di tre variabili in forma canonica:
Sia data la funzione
espressa dalla seguente tavola della verità:
La
forma canonica di primo tipo (somma di minterm), che andremo a prediligere, si ottiene col seguente procedimento:
-
Si considerano tutte le righe della tabella per le quali
-
Si scrive una somma di tanti minterm quante sono le righe individuate da . In ogni minterm si negano le variabili che, nella tabella, sulla riga considerata, sono pari a 0.
Nel nostro caso si ottiene:
Si noti che, spesso, le funzioni logiche possono essere minimizzabili. Nel nostro caso possiamo notare che:
. Questo procedimento può esser laborioso e sono stati sviluppati dei metodi che consentono una maggior semplicità di minimizzazione. Tale argomento verrà affrontato nel seguito.
Per ottenere la
forma canonica del secondo tipo (prodotto di maxterm) si procede in modo duale:
-
Si considerano tutte le righe della tabella per le quali
-
Si scrive un prodotto di tanti maxterm quante sono le righe individuate da . In ogni maxterm si negano le variabili che, nella tabella, sulla riga considerata, sono pari a 1.
Nel nostro caso si ottiene:
Diamo, qui oltre, alcune definizioni:
-
Implicante. Si definisce implicante di una funzione booleana qualsiasi prodotto parziale fra le variabili che, quando è pari a 1, rende uguale a 1 anche la funzione stessa.
-
Implicante primo. Si definisce implicante primo ogni implicante non contenuto in altri implicanti.
-
Forma non ridondante è la somma di implicanti primi che contiene tutti i minterm della funzione.
-
Implicante essenziale è ogni implicante primo che compare in ogni forma non ridondante di una funzione booleana e che la descrive compiutamente.
2.2
Il Teorema di Espansione
Introdotto da Boole nel 1847 prende, spesso, il nome di
Teorema di Espansione di Shannon ed asserisce che:
sia una funzione booleana di n variabili. Allora per tutti gli in si ha:
Ne omettiamo la dimostrazione.
Il teorema di espansione permette di ottenere un'espressione in forma cano-nica per ogni funzione booleana, ovvero ogni funzione booleana può essere espressa mediante la somma di tutti i minterm ai quali si associa un coefficiente pari al valore che la funzione assume sostituendovi ciascuna variabile con
1 se nel minterm appare in forma diretta o con
0 se compare in forma negata. In altre parole, ogni minterm viene moltiplicato per il coefficiente
1 se fa parte della funzione o per
0 in caso contrario.
Analogamente la forma canonica di secondo tipo di una funzione booleana è pari al prodotto di tutti i maxterm: ad ogni maxterm si somma
0 se fa parte della funzione o
1 in caso contrario.
Si noti che, essendo i termini canonici
, il numero di funzioni canoniche di
n variabiliè pari a quello delle variazioni con ripetizione dei due elementi
0 e
1 presi di
in
, ossia a
. Ad esempio, per 3 variabili si possono scrivere
funzioni canoniche.
3
Semplificazione delle funzioni logiche
Prima di procedere alla realizzazionefisica delle funzioni logiche, è bene semplificare le stesse in modo da poterle rappresentare col minor numero di componenti. Sebbene non esista un criterio unico per minimizzare le funzioni, esistono, invece, metodi rigorosamente oggettivi che consentono di pervenire all'espressione
minima, ovvero non ulteriormente riducibile, della funzione logica di cui trattasi.
I due metodi principali, di cui vedremo solo il primo, sono le
mappe di Karnaugh e il
metodo di Quine e McCluskey.
3.1
Le Mappe di Karnaugh
Inventate nel 1953 da Maurice Karnaugh, ingegnere elettronico in telecomunicazioni dei Bell Laboratories, trovano semplice applicazione per funzioni fino a quattro variabili, oltre le quali vedrebbero una rappresentazione tridimensionale di scarso utilizzo pratico, o ancora usare altre mappe supplementari in più il cui numero cresce in maniera esponenziale per ogni variabile oltre la quarta. Il numero di tali combinazioni è
, in cui
n è il numero di variabili della funzione: ad esempio 5 variabili necessitano di 2 mappe, 6 variabili necessitano di 4 mappe, mentre 7 variabili necessitano di 8 mappe...
Il principio per la costruzione delle mappe trae origine dalla considerazione che coppie di termini adiacenti possono essere ridotte ad un solo termine nel quale si è eliminata la variabile che cambia stato all'interno delle coppie mede-sime (
).
La costruzione delle mappe parte riunendo i termini adiacenti in modo che siano fisicamente contigui, al fine di semplificare la procedura di riduzione delle variabili.
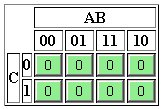
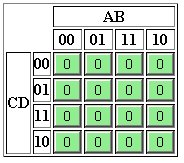
Vengono costruite tramite una tabella contenente tante celle quante sono le combinazioni possibili delle variabili contenute nella funzione logica. Sui lati della tabella si riportano, come coordinate, le combinazioni di variabili che identificano ogni quadretto interno, facendo in modo che i valori cambino
uno solo per volta (
distanza di Hamming unitaria).
Reticoli per la costruzione di mappe di Karnaugh a 2, 3 e 4 variabili.
Per poter vantaggiosamente utilizzare le mappe di Karnaugh, queste devono essere considerate come superfici chiuse, sviluppate sul piano, quindi le celle della prima riga sono adiacenti a quelle dell'ultima così come quelle della prima colonna sono adiacenti a quelle dell'ultima.
Una volta costruita la mappa di Karnaugh, per ottenere l'espressione mi-nima della funzione, occorre individuare tutti i massimi gruppi di celle contenenti
1 ed aventi un numero di celle per lato che sia una potenza di 2, in modo da considerare almeno una volta tutti gli
1 presenti. Alcuni gruppi possono essere parzialmente sovrapposti. Se si trovano più possibilità si scelgono i raggruppamenti più grandi.
Nelle figure a seguire indicheremo diversi raggruppamenti, ognuno con la funzione logica che lo ha generato e la funzione minima.
Le immagini sono state generate dall'applicazione online reperibile alla URL:
http://www.ee.calpoly.edu/media/uploads/resources/KarnaughExplorer_1.html
4
Porte Logiche Integrate e Logica Combinatoria
4.1
AND (prodotto logico)
La porta AND (&) serve ad eseguire, su segnali elettrici, l'operazione di prodotto logico.
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
4.2
OR (somma logica)
La porta OR (+) serve ad eseguire, su segnali elettrici, l'operazione di somma logica.
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
4.3
NOT (negazione)
La porta NOT (-) serve ad eseguire, su segnali elettrici, l'operazione di inversione logica.
A differenza delle altre porte, ha sempre e solo un unico ingresso.
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
4.4
NAND (prodotto negato)
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
E' facile osservare come una NAND con gli ingressi cortocircuitati realizzi una NOT.
4.5
NOR (somma negata)
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
4.6
EX-OR (somma esclusiva)
La porta EX-OR
serve ad eseguire sui segnali elettrici la funzione di somma esclusiva.
Di notevole importanza pratica (l'uscita è alta se e solo se gli ingressi sono diversi), realizza la funzione logica
. La sua realizzazione, in un circuito realizzato sfruttando il teorema di De Morgan e, quindi, utilizzando solo porte NAND, è il seguente:
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
4.7
EX-NOR (somma esclusiva negata)
Come è facilmente dimostrabile, realizza la funzione logica
, la cui dimostrazione è lasciata all'attento lettore.
Nelle illustrazioni, il simbolo circuitale e la relativa tabella della verità.
4.8
Half Adder (semisommatore)
Una delle principali applicazioni della porta EX-OR è nella realizzazione di circuiti che eseguano la somma fra due numeri binari.
Le regole di somma sono riportate nella tabella sottostante, in cui con il simbolo
si indica la somma, mentre, con il simbolo
R il riporto:
Un circuito, adatto a sommare le cifre meno significative di un numero binario, è il seguente:
Tale circuito non tiene, però, in conto dell'eventuale resto di una precedente somma.
4.9
Full Adder (sommatore)
A differenza dell'
half adder, il
full adder è in grado di avere, in ingresso, il riporto della somma fra le due cifre precedenti.
Detto
il riporto dell'operazione precedente ed
il riporto attuale, la tavola della verità è la seguente:
Da questa si ricavano le espressioni di
e di
:
Il circuito che realizza questa funzione è qui riportato:
4.10
Comparatori
Con l'uso delle porte
EX-OR ed
EX-NOR è semplice realizzare circuiti in grado di confrontare due numeri binari.
Nell'esempio di figura, siano da confrontare due numeri binari espressi con 4 bit:
e
. Ogni singolo bit viene comparato, tramite la relativa porta
EX-NOR, con il bit corrispondente dell'altro numero. Le uscite delle
EX-NOR saranno tutte alte se e solo se ogni singolo bit è uguale al suo corrispondente e, quindi, l'uscita del circuito sarà alta se i numeri sono uguali.
4.11
Convertitori di codice
Supponiamo di dover convertire un numero binario, su 3 bit, nell'equivalente codice decimale, su 8 bit.
La tavola della verità di tale funzione sarà la seguente in cui
sono i bit d'ingresso e
le uscite:
Il circuito sarà il seguente:
4.12
Selettori di canale (multiplexer)
Il selettore di canale più semplice realizza la funzione
ed, in questo caso, sceglie fra due soli canali,
A e
B ed in cui la variabile
M è la variabile di scelta.
Il circuito è riportato nella figura seguente:
Con un convertitore di codice ed estendendo la relazione vista per un selettore a due canali, possiamo ottenere un
multiplexer a
n canali. Nell'illustrazione seguente è realizzato un selettore a 8 canali. Il canale che si intende inviare all'uscita viene scelto impostando un numero binario agli ingressi di controllo.
5
Circuiti sequenziali
I circuiti sequenziali, come dice il termine, sono quelli in cui, a differenza dei circuiti combinatori, il
tempo prende parte attiva al funzionamento del dispositivo.
5.1
Flip - Flop
Il più semplice circuito sequenziale è il
multivibratore bistabile o
flip flop. Viene realizzato connettendo ad anello due porte invertenti in modo da avere una reazione positiva.
Consideriamo il caso in cui in un istante
si abbia
S=R=0. Essendo il circuito costituito da porte NOR e, ricordando che lo
0 è l'elemento neutro della somma, gli ingressi S ed R non controllano lo stato delle uscite che, quindi, dipendono solo dagli altri ingressi e, quindi, dalle uscite nell'istante
precedente.
Possiamo facilmente verificare che, se le uscite erano tra loro complentari, ovvero se
, portare sia S che R a 0 lascia inalterata la situazione precedentemente acquisita. Si dice che per
S=R=0 il Flip-Flop sia in condizione di
memoria. Se, al contrario, nell'istante
si avesse avuto
, ad esempio a livello basso, portando, all'istante
gli ingressi in condizione di memoria, lo stato risultante del Flip-Flop sarebbe stato imprevedibile, dipendendo da quale ingresso,
R o
S, fosse stato portato per primo a “
0”. Per questo motivo la condizione
S=R=1, che comporta uscite non complementari, è considerata
Vietata.
Se
R=1, allora
U=0 e
U'=1. Se, invece, è l'ingresso
S ad essere portato alto, la situazione si inverte:
U=1 e
U'=0. Siccome si ha sempre
si è soliti chiamare
e
. Il Flip-Flop ha, quindi, due stati stabili, corrispondenti a
Q=0 (stato di
RESET) e
Q=1 (stato di
SET)
Per questo motivo tale dispositivo prende il nome di
SRFF ovvero di
Flip-Flop Set-Reset.
Simbolo circuitale e tavola della verità sono appresso riportati
5.2
Flip Flop Sincronizzati
5.2.1
Flip-Flop Master - Slave
Le commutazioni delle uscite
Q e
nel SRFF avvengono solo allorquando agli ingressi si realizzino le condizioni adatte. In realtà, nella pratica comune, occorre che le commutazioni avvengano contemporaneamente ovvero che siano
sincronizzate ad un ben preciso istante.
Tale istante, generalmente, coincide con i fronti di salita o di discesa di un segnale detto
clock.
Un Flip - Flop di questo tipo si basa sul principio del
Master - Slave ed il circuito che lo realizza è rappresentato in figura:
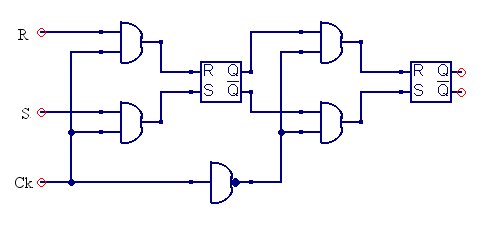
Consideriamo un istante in cui il segnale di clock (Ck) sia “alto” (1 logico). In questa situazione le porte AND all'ingresso del primo SRFF sono abilitate mentre quelle all'ingresso del secondo sono inibite. In tali condizioni i segnali
S ed
R all'ingresso del circuito si troveranno sui morsetti del primo SRFF che andrà in acquisizione, mentre il secondo SRFF vedrà in ingresso due 0 logici e sarà nello stato di memoria, presentando all'uscita del circuito il valore che già deteneva. Nel momento in cui il segnale di clock si porterà allo stato “basso” (0 logico), sul fronte di discesa, sarà il primo flip-flop a passare in memoria mentre il secondo acquisirà i valori delle uscite del primo e li presenterà all'uscita. Possiamo dire, quindi, che l'intero complesso
Master - Slave acquisisce sul fronte di salita e commuta sul fronte di discesa. Questo passaggio fra ingresso ed uscita, che avviene in due tempi, è l'elemento fondamentale del funzionamento del
Master - Slave e consente di realizzare i flip-flop JK, che troviamo normalmente integrati, e che saranno oggetto della prossima sottosezione.
5.2.2
Flip - Flop JK
I Flip-Flop visti sinora hanno una condizione non permessa in ingresso, ovvero quando entrambi i segnali sono ad “
1”. Il Flip-Flop JK (
JKFF) dà un significato a questa combinazione e la presenza di una simile combinazione ha l'effetto di far commutare le uscite
Q e
sul fronte di discesa del clock qualunque fosse il vaslore dell'uscita all'istante precedente:
La tavola della verità di questo dispositivo è la seguente:
Consideriamo il caso in cui entrambi gli ingressi e il clock siano “alti”: le prime prime porte AND sono abilitate ed il valore delle uscite si presenta “
invertito” all'ingresso, nel senso che il valore dell'uscita
Q si troverà all'ingresso
K e il valore di
su
J. Il primo SRFF acquisirà questi valori mentre il secondo sarà in condizione di memoria. Sul fronte di discesa del clock il primo SRFF passerà in memoria, chiudendosi le porte al suo ingresso, ed il secondo acquisirà le sue uscite, di fatto commutando le uscite dell'intero circuito. Quindi, all'istante
,
Q presenterà il valore di
dell'istante precedente
e viceversa.
Il simbolo circuitale del JKFF è qui rappresentato:
In questo simbolo sono presenti due ingressi
asincroni:
Clr (
Clear) e
Pr (
Preset), tavolta indicati anche dalle lettere
S (
Set) ed
R (
Reset). Questi consentono di “forzare” in uscita una determinata condizione desiderata indipendentemente dallo stato del clock. Portando l'ingresso relativo del
Clr a “0” si forza Q a “0”, mentre portando a “0” il Preset si forza Q ad “1” (si osservi che gli ingressi asincroni sono negati).
Il “pallino” sull'ingresso del clock sta ad indicare che il JKFF acquisisce sul fronte di discesa.
Direttamente dal JKFF discendono i prossimi due tipi di Flip-Flop.
5.2.3
Flip-Flop di tipo “D”
Il Flip-Flop di tipo “D”, dove
D, a seconda degli autori, sta sia per “
Data” (dato) che per “
Delay” (ritardo) è ottenuto dal JKFF semplicemente negandone gli ingressi:
Le applicazioni del DFF sono prevalentemente legate al suo utilizzo come “
latch”, cioè come circuito che memorizzi il valore di un segnale in un ben determinato istante. L'istante della temporizzazione è dato dal fronte di salita o di discesa del clock. La sua tavola della verità è appresso indicata:
Nella tabella il simbolo
indica il fronte di discesa del clock, mentre la lettera “
X” sta ad indicare uno stato indifferente.
La figura seguente rappresenta lo schema di un Flip-Flop integrato di tipo commerciale, della famiglia 7474, realizzato a sole porte NAND.
5.2.4
Flip-Flop di tipo “T”
Il Flip-Flop di tipo “T”, dove
T sta per “Toggle” (commutazione) è ottenuto dal JKFF semplicemente connettendone gli ingressi in corto.
Ha un ingresso, due uscite complementari e un ingresso di sincronizzazione. Ha funzioni di memoria e commutazione, che consiste nella negazione del valore precedentemente memorizzato.
Se
T è “alto”, ad ogni fronte di discesa del clock, le uscite commutano lo stato, se
T è a “0” il TFF è in memoria.
5.3
Contatori
Un contatore è un circuito sequenziale, realizzato tramite Flip-Flop, utilizzato per contare il numero di impulsi applicati al suo ingresso.
I contatori si differenziano sia per il codice con il quale rappresentano il numero conteggiato, sia per il fatto di essere sincroni o asincroni.
Siccome ogni Flip-Flop ha due stati distinti, il numero degli stati di un contatore costituito da
n Flip-Flop sarà
. Quindi un contatore potrà rappresentare un massimo di
numeri, da
0 a
.
Un contatore ad
S stati viene anche definito “
contatore modulo S”.
5.3.1
Contatori binari asincroni up
I contatori binari asincroni sono costituiti da Flip-Flop di tipo T connessi in cascata, ognuno commuta sul fronte di discesa dell'uscita del precedente ed il primo commuta sul fronte di discesa del clock.
Il diagramma temporale è rappresentato nell'illustrazione che segue. E' facile riconoscere il codice binario in cui l'uscita
A costituisce il bit meno significativo (
LSB -
Least Significant Bit) mentre
C è il bit più significativo (
Most Significant Bit).
Il contatore raffigurato è costituito da tre Flip-Flop ed è, quindi, un contatore
modulo 8, ovvero è in grado di contare da 0 a 7 per poi tornare allo stato iniziale in cui
A=B=C=0 per ricominciare il ciclo da capo.
Uso caratteristico di un simile contatore è quello di divisore di frequenza. Se osserviamo la figura sottostante vediamo che l'uscita di ogni TFF ha una frequenza pari alla metà di quella al suo ingresso e, quindi, l'uscita di un contatore binario puro è sempre una frequenza sottomoltipla di due della frequenza del segnale originale.
In questo tipo di contatori ogni impulso in ingresso incrementa di uno il numero binario rappresentato. Per questo motivo vengono chiamati “
contatori binari asincroni up” o “
avanti”.
5.3.2
Contatori binari asincroni down
Se, anziché l'uscita
Q si sfrutta l'uscita
per essere collegata al clock del TFF successivo, si hanno contatori che decrementano di un'unità il numero binario indicato come conteggio. In tal caso parleremo di “
contatori binari asincroni down”. Un esempio è rappresentato nella figura che segue:
La comprensione del funzionamento è banale se pensiamo che il fronte di salita di
Q corrisponde al fronte di discesa di
e diventa ancora più semplice osservando il diagramma temporale rappresentato nella figura seguente:
E' immediato riconoscere un codice binario che, partendo dal 7 (111) va via via decrementandosi fino a 0 (000). Anche in questo caso A sarà il LSB e C il MSB.
5.3.3
Contatori binari asincroni up & down
Riunendo i due circuiti visti in precedenza ed abilitando le uscite di ogni TFF tramite un multiplexer 2 x 1 si ottiene il circuito in figura, noto come “
contatore binario asincrono up & down”.
I contatori sopra descritti prendono anche il nome di “
ripple counter” (letteralmente
contatori ad ondulazione), o “
asincroni”, in quanto non esiste un segnale di clock comune a tutti i Flip-Flop: ogni TFF riceve il segnale di comando dalla commutazione del Flip-Flop precedente. Ciò implica che non si abbia una commutazione istantanea di tutte le uscite me sia presente un ritardo di propagazione dovuto ai ritardi introdotti dai vari TFF.
Il caso peggiore si palesa allorquando tutti i TFF del circuito devono commutare, ad esempio, per il contatore “up”, all'arrivo del quarto impulso. In questo caso l'ultima uscita cambia stato dopo un tempo
dall'arrivo del comando in ingresso, in cui “
n” è il numero di TFF e
è il ritardo di propagazione di ogni singolo TFF.
Se si desidera leggere, senza errori, il risultato, occorre attendere un tempo pari ad almeno
dopo il fronte attivo in ingresso, per essere sicuri che le uscite siano stabili. Questo fatto provoca una limitazione alla frequenza massima di conteggio. Definendo con
il tempo necessario alla lettura del dato, l'intervallo di tempo fra due dati seguenti dovrà risultare
. Dovendo, invece, utilizzare i contatori come divisori di frequenza, questa limitazione viene a cadere.
5.3.4
Contatori binari sincroni
E' possibile ridurre gli effetti del ritardo di propagazione utilizzando dei contatori “
sincroni” in cui tutti i Flip-Flop sono comandati simultaneamente dallo stesso segnale di clock, mentre, utilizzando gli ingressi
T, si condiziona la commutazione del Flip-Flop a seconda dello stato precedente delle uscite del contatore.
In questo circuito l'ingresso di abilitazione “
E” (
enable) è portato ad “
1” ed il primo TFF commuta sempre sul fronte di discesa dell'ingresso, mentre i successivi commutano solo quando le uscite del Flip-Flop precedente sono alte. L'uscita “
Tc” (
terminal count” consente di connettere più contatori in cascata al fine di aumentare la capacità di conteggio. In questo caso l'uscita
Tc di ogni conattore viene connessa all'ingresso
E del successivo in modo che la commutazione avvenga solo quando tutte le uscite del primo siano alte. L'uscita
Tc prende il nome di “
Carry” (
riporto) se si tratta di un contatore
up e di “
Borrow” (
prestito) per un contatore
down.
5.3.5
Le funzioni di controllo “Preset” e “Reset”
La funzione di “Reset” consiste nel portare tutti i Flip-Flop JK del contatore allo stato “0”. Questa operazione assicura che il contatore inizi il conteggio dallo stato in cui indica il numero “0”. Per ottenere questa funzione, possiamo utilizzare gli ingressi di “Clear” e di “Preset” dei JKFF portando a “0” logico per un determinato periodo di tempo, normalmente pari a 100 nS per le logiche TTL, la linea
. Quando questa è ad uno stato alto, il contatore funziona normalmente.
L'operazione di “
Preset” consiste nel caricare un dato numero binario nel contatore prima che questo cominci a contare, in modo che il conteggio abbia inizio da un numero determinato. Questo numero viene ad essere presentato agli ingressi di
Preset. Quando la linea
Preset viene portata ad “1” si abilitano le porte relative ed, essendo gli ingressi
S attivi sullo “0” logico, gli ingressi di
Preset ad “1” forzano un'uscita “alta” al JKFF relativo.
Al contrario, degli “0” sugli ingressi di
Preset non possono modificare il contenuto del Flip-Flop. Per questo motivo è sempre necessario far precedere all'operazione di
Preset un'operazione di
Reset, in modo da azzerare preventivamente tutte le uscite.
Nell'illustrazione seguente è rappresentato un circuito in grado di ottenere indipendentemente entrambe le operazioni di
Preset e di
Reset: il dato presente sull'ingresso di
Preset viene portato sia sull'ingresso
S che, negato, sull'ingresso
R. Ovviamente, tale circuito verrà replicato su ogni JKFF.
5.3.6
Contatori in codice BCD
Sono circuiti sequenziali che contano per dieci con la seguente sequenza (DCBA):
La figura seguente rappresenta una realizzazione di un contatore decimale asincrono o, come normalmente viene chiamato, di una
decade asincrona.
Il diagramma temporale è qui appresso riportato:
Il segnale proveniente da
(uscita
) viene riproposto all'ingresso
del secondo JKFF, la porta
AND effettua il prodotto logico fra
B e
C per comandare la commutazione dell'ultimo JKFF.
Il primo JKFF commuta ad ogni fronte di discesa dell'ingresso, il secondo JKFF (uscita B) commuta su ogni fronte di discesa di A tranne al decimo impulso, quando, essendo
e
,
e
. In queste condizioni il secondo JKFF non commuta. Il terzo JKFF (uscita C) commuta su ogni fronte di discesa di B mentre l'ultimo JKFF (uscita D) commuta sui fronti di discesa di A solo se
C=B=1 ovvero all'ottavo impulso e al decimo impulso quando, essendo
e
l'uscita si porta nello stato basso.
5.4
I registri a scorrimento (Shift Register)
Sono circuiti costituiti da elementi di memoria disposti in cascata in modo che l'informazione possa venir spostata da ogni elemento a quello adiacente tramite un comando di clock.
Vedono le loro più frequenti applicazioni come memorie seriali, convertitori parallelo-serie e serie-parallelo, contatori ad anello, come elementi di calcolo aritmetico e nella conversione analogico decimale ad approssimazioni successive.
Gli shift register bipolari sono, generalmente, costituiti da JKFF, talvolta da DFF. In tecnologia MOS, grazie alla loro bassissima potenza dissipata, costituiscono il tipo con la maggior densità di integrazione e realizzano gli shift register più lunghi.
5.4.1
Shift Register Bipolari - convertitore SISO
Un tipico registro a scorrimento è rappresentato nell'illustrazione seguente:
Lo shift register è un circuito sincrono, in quanto tutti i flip-flop ricevono lo stesso segnale di clock.
L'immagine seguente ci spiega come venga caricata una parola seriale:
Ad ogni fronte di discesa del Clock il JKFF successivo acquisisce l'uscita del JKFF precedente. Dopo
n impulsi di clock, con
n pari al numero di JKFF presenti nel registro, all'uscita sarà emessa la parola inserita in ingresso.
Questo tipo di registro è, quindi, un convertitore
SISO:
Serial Input Serial Output, o convertitore Serie-Serie.
5.4.2
Shift Register Bipolari - convertitore SIPO
I dati vengono inseriti nello shift register in modo seriale, uno per ogni impulso di clock, e letti tutti contemporaneamente, e quindi in parallelo, sulle uscite dopo
n impulsi di clock, una volta che la lettura venga abilitata portando ad “1” lo stato dell'ingresso
E di abilitazione. In questo caso la conversione è di tipo Serie-Parallelo ovvero
SIPO:
Serial Input Parallel Output.
Il circuito relativo è appresso raffigurato.
5.4.3
Shift Register Bipolari - convertitore PISO
Questo genere di convertitori sfrutta gli ingressi asincroni: il dato viene presentato in parallelo ai pin indicati come “
In” e, grazie ad un apposito comando di “
Load”, viene caricato nei singoli JKFF. Ad ogni impulso di clock la parola si presenta in uscita in modalità seriale. Abbiamo così realizzato un convertitore Parallelo-Serie ovvero
PISO: Serial Input Parallel Output. Il circuito relativo è in figura:
Esistono, infine, shift register in cui è possibile, tramite un apposito comando, invertire il senso di scorrimento.