Maurizio Monteduro - Maria Grazia Trivi

• Generalità sugli amplificatori per grandezze continue
• Stadio d'ingresso
• L'amplificatore differenziale
• Transcaratteristica
• Dinamica d'ingresso per il modo comune
• Offsets dello stadio differenziale
• Criteri per la realizzazione di un amplificatore per grandezze continue
• Stadio intermedio
• Stadio finale

Definiamo correntemente "AMPLIFICATORI PER GRANDEZZE CONTINUE" i dispositivi in grado di rilevare variazioni molto lente di un segnale (tensione o corrente) in ingresso e di tradurle in variazioni proporzionali ai morsetti di uscita.

Le variazioni all'ingresso vanno intese rispetto ad un livello nominale di riferimento e pertanto daranno luogo a variazioni corrispondenti in uscita.

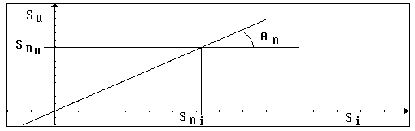
Detto S_i il segnale in ingresso ed S_u quello in uscita, supponendo che l'amplificatore lavori in zona lineare, la sua funzione di trasferimento nel piano S_i vs S_u è una retta individuata perfettamente da un suo punto e dalla sua pendenza. Le coordinate scelte per individuare la retta, vengono chiamate "LIVELLO NOMINALE DI INGRESSO S_ni" e "LIVELLO NOMINALE DI USCITA S_nu". La pendenza A_n rappresenta l'amplificazione.

Stando così le cose, pensiamo di poter progettare un amplificatore determinando la funzione di trasferimento (FdT) nominale e, quindi, i livelli nominali di riferimento e l'amplificazione. In realtà, in fase di realizzazione, intervengono le tolleranze degli elementi, attivi o passivi, che realizzano il circuito. In altri termini, la FdT reale, si discosterà dalla FdT nominale, ovvero, se ponessimo all'ingresso del nostro dispositivo reale, posto nelle condizioni nominali di temperatura, di tensione d'alimentazione, ecc. un segnale di livello nominale S_ni otterremmo in uscita un segnale S_ru diverso dal segnale nominale S_nu, così come illustrato in figura:

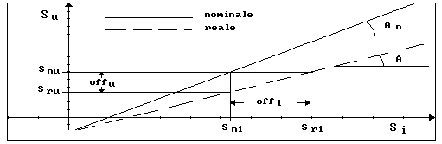
Definiamo "Offset in Uscita" la grandezza:

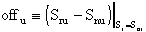
Rimanendo nelle condizioni nominali di temperatura e di alimentazione, variamo il segnale in ingresso sino ad un valore S_ri per il quale l'uscita raggiunge il suo valore nominale S_nu. Possiamo così definire la grandezza "Offset in Ingresso" secondo la seguente relazione:

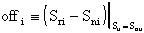
Resta evidente chei due offsets saranno legati dal fatto che

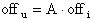
Col variare della temperatura, o della tensione d'alimentazione, o a causa dell'invecchiamento del circuito, varieranno anche gli offsets.

Definiamo "DERIVE" (drifts) le variazioni degli offsets.

Gli offsets e le derive sono indistinguibili dalle variazioni del segnale in ingresso, ma, mentre è semplice, circuitalmente parlando, "recuperare" gli offsets, risulta più difficile annullare, o compensare, gli effetti delle derive. Risulta inoltre evidente che sia gli offsets che le derive, quando siano "mischiati" col segnale d'ingresso, subiranno le stesse manipolazioni seguite da quest'ultimo e quindi, generalmente, verranno anch'essi amplificati.

Sebbene tutti gli elementi circuitali, attivi e passivi, presentino delle derive termiche, ciò che ci dà maggiormente fastidio in un amplificatore sono le derive degli elementi attivi.

Infatti ricordiamo che, per un transistor bipolare, valgono le seguenti relazioni approssimate:

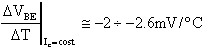
ossia, la V_BE, diminuisce di circa 2 mV per ogni aumento, nella temperatura, di un grado centigrado.

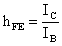
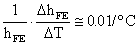
ovvero cresce, con la temperatura, dell' 1% al grado centigrado e diminuisce con l'invecchiamento.

Ricordando che I_CBO è la corrente inversa collettore-base con l'emettitore aperto, ovvero, corrente inversa di saturazione della giunzione base-collettore, osserviamo che:

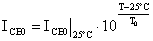in cui T₀=30° ÷ 50° per il Silicio

T₀=25° ÷ 30° per il Germanio

quindi I_CBO raddoppia approssimativamente ogni 10°C; inoltre cresce con l'invecchiamento del componente.

Come è noto, tutte tre queste sorgenti di derive termiche concorrono a far aumentare la corrente I_C di collettore al crescere della temperatura, quindi non possiamo sperare che si compensino da sole.

Torna all'indice

Consideriamo in primo luogo gli effetti della V_BE. Abbiamo visto che essa varia con la temperatura. Agli effetti della maglia d'ingresso di un qualsiasi transistor, questo può essere visto come la serie di un transistor ideale, senza variazioni della V_BE, e di un generatore di tensione di valore

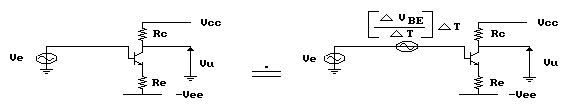
Questo generatore di deriva, si trova connesso direttamente in serie al segnale da amplificare V_e, quindi, per il solo contributo della V_BE la deriva d'ingresso è pari a circa -2,5 mV/°C. Le altre fonti di deriva (I_CBO e h_FE) Peggioreranno solamente la situazione.

Giunti a questo punto, pensiamo di introdurre nella maglia d'ingresso un elemento che abbia le stesse variazioni della giunzione base-emettitore del transistor, connettendolo in modo tale che le due derive si annullino. Utilizziamo un diodo.

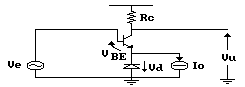
È evidente che, per poter funzionare, il diodo deve essere polarizzato, quindi occorre un qualcosa che possa "succhiare" le correnti, sia quella che arriva dall'emettitore del transistor, sia quella che serve a polarizzare il diodo stesso. Questo "qualcosa" è rappresentato dal generatore ideale di corrente I₀ posto in parallelo al diodo medesimo.

Se si sostituisce al diodo la giunzione base-emettitore di un transistor, si ottiene il circuito riportato nelle figure seguenti, in cui è facile riconoscere uno stadio differenziale.

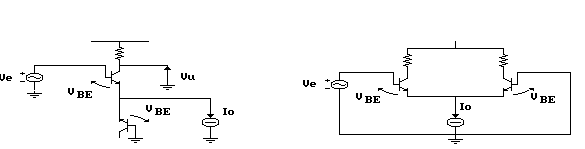
Vedremo, in seguito, come l'amplificatore differenziale amplifichi la differenza dei segnali d'ingresso e come, riportando sulla base dei due transistori le rispettive derive, essendo queste identiche, possa compensarle. L'amplificatore differenziale permette così di ottenere derive riferite all'ingresso dell'ordine dei 10 V/°C, ed è quindi un ottimo stadio d'ingresso per un amplificatore per grandezze continue.

Torna all'indice

Prima di affrontare lo studio dettagliato del circuito dello stadio differenziale, facciamo alcune considerazioni di carattere generale.

Siano V₁ e V₂ due segnali, possiamo dire facilmente che:

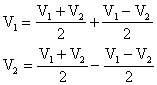
Definendo, ora:

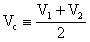
e

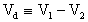
possiamo notare che:

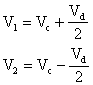
Raffigurando queste formule, otterremo:

Chiamiamo V_c = SEGNALE di MODO COMUNE e V_d = SEGNALE di MODO DIFFERENZIALE.

É evidente, che potrò sempre attuare una scomposizione di questo genere, per qualsiasi combinazione dei segnali in ingresso ad un amplificatore differenziale.

Se il nostro circuito è in linearità, è possibile utilizzare il principio di sovrapposizione degli effetti e valutare la risposta complessiva del circuito, per mezzo della somma dei contributi dei due modi di eccitazione.

Definiamo AMPLIFICAZIONE DIFFERENZIALE il termine:

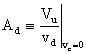
e AMPLIFICAZIONE di MODO COMUNE il termine:

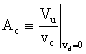
Allora V_u sarà la somma di V_c per l'amplificazione A_c e di V_d per l'amplificazione Ad:

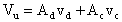
In un amplificatore differenziale ideale, il termine A_c è uguale a 0; ma il fatto che qui ci si occupi di amplificatori reali, giustifica la relazione appena vista in cui, riarrangiando, posso mettere in evidenza A_d v_d, ottenendo:

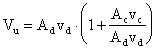
da cui

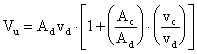
Si vede chiaramente che, minore è il termine (ovvero maggiore è ) e minore è l'errore dovuto al modo comune.

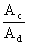
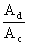
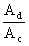
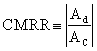
Il rapporto viene definito Rapporto di Reiezione del Modo Comune ( Common Mode Rejection Ratio ) e può essere considerato una "cifra di merito" dell'amplificatore differenziale. Quindi:

Conoscendo le amplificazioni A_d e A_C in decibel, è facile esprimere il CMRR come loro somma algebrica:

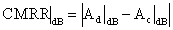
Occorre sottolineare che, in quanto è stato illustrato sinora, si presume la linearità del circuito, linearità che, generalmente, è verificata con piccoli segnali in ingresso. Molto spesso, tali segnali provengono da sensori, quindi ci si può trovare nella situazione di dover lavorare con piccoli segnali differenziali, sovrapposti a forti segnali di modo comune. Dobbiamo, allora, essere certi che il modo comune presente non porti fuori linearità l'amplificatore.

Si definisce come "Dinamica d'Ingresso per il Modo Comune" (Common Mode Imput Range = CMRI), il campo di tensione in cui può variare un segnale di modo comune senza che intervengano fenomeni di non linearità, ovvero senza che i transistori si saturino o si interdicano. In modo del tutto simile si può definire la "Dinamica d'Ingresso Differenziale" (Differential Mode Input Range = DMIR).

Torna all'indice

Pensiamo ora di ricavare la caratteristica di trasferimento di un amplificatore differenziale, realizzato con transistors bipolari.

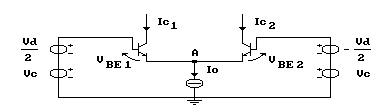
Supponiamo che i due transistors siano identici e siano alla stessa temperatura, ciò significa che essi hanno lo stesso fattore di amplificazione in corrente ß e la stessa corrente inversa di saturazione della giunzione base-emettitore I_S, inoltre le derive termiche sono le stesse per entrambe i componenti. Quindi scrivendo l'equazione alla maglia d'ingresso del circuito in Figura otteniamo:

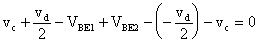da cui

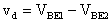
Sapendo che il transistor può essere rappresentato, tramite il modello di Ebers-Moll, come la connessione di due diodi di cui, uno polarizzato direttamente (giunzione B-E) e l'altro inversamente (giunzione B-C); possiamo dire che, per la corrente di emettitore I_E, vale la seguente relazione:

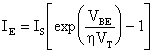
in cui 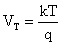con: k = costante di Boltzmann = 1,381·10^-23 J/°K

q = carica dell'elettrone = 1,602·10^-19 C

T = temperatura assoluta in gradi Kelvin

I_E = corrente di emettitore;

I_S = corrente inversa di saturazione della giunzione base-emettitore;

h è un fattore che dipende dal tipo di semiconduttore usato: vale circa 2 per il Silicio e circa 1 per il Germanio. Tali valori sono corretti solo per bassi livelli di corrente, ma tenendo presente che la corrente di emettitore è di almeno 6 ordini di grandezza superiore alla corrente inversa di saturazione, allora, per il Silicio, dobbiamo considerare h@1.

[ ; a 25 °C (298.16 °K), V_T = 25.703 mV @ 26mV ]

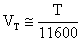
Dopo le considerazioni svolte e tenendo presente che, per V_BE ³ 5V_T, l'unità è da considerarsi trascurabile rispetto all'esponenziale, possiamo scrivere:

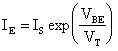
dalla quale si deduce che:

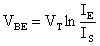
Allora:

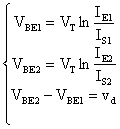
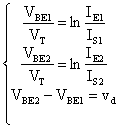
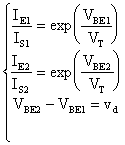
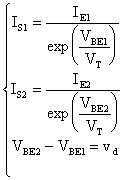
siccome I_S1 = I_S2, confrontando le prime due equazioni del sistema, otteniamo:

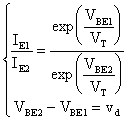
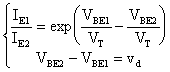
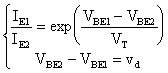
infine ricaviamo:

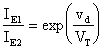
Inoltre, dall'equazione al nodo A, possiamo dire:

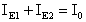
Mettendo a sistema le due equazioni:

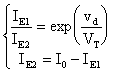
otteniamo:

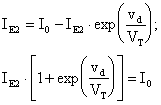
da cui

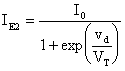
In modo del tutto analogo ricaviamo:

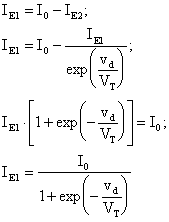
Si può notare che, avendo ipotizzato i transistors identici e il generatore di corrente I₀ ideale, il segnale di modo comune non influenza nè le correnti di emettitore, nè, di conseguenza, nemmeno quelle di collettore dei due componenti.

Riunendo in un solo grafico le equazioni relative ad I_E1 e ad I_E2 avremo la figura seguente che fornisce la transcaratteristica dell'amplificatore differenziale.

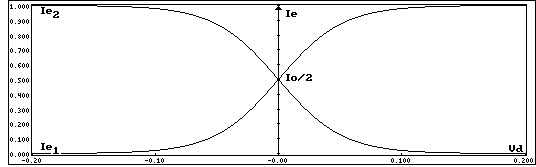
Dalla sua analisi, vediamo che il circuito si può pensare in linearità solo per un segnale v_d in ingresso, compreso fra ± V_T, ovvero fra ± 26 mV (alcuni autori, fra cui J.Millmann, ampliano la zona di linearità comprendendo ± 2 V_T, cioè ± 52 mV). Inoltre si nota che i transistors vanno in saturazione se v_d supera ± 100 mV (circa 4V_T). Si comprende quindi, come il segnale d'ingresso, di uno stadio differenziale, non possa superare i limiti di ± 26 mV

(ovvero ± 52 mV).

Definiamo ora la transconduttanza dell'amplificatore; analiticamente essa sarà data dall'espressione:

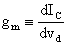
Ricordiamo che:

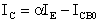
dove: 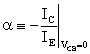; il suo valore tipico è circa uguale a 1 o, più precisamente: 0,95 £ a £ 0,998.

I_CBO è la corrente inversa di saturazione della giunzione base-collettore, e può essere trascurata in quanto il suo valore è molto piccolo rispetto alla corrente di emettitore.

Allora sostituendo e trascurando I_CBO otteniamo:

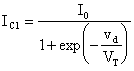
Applicando ora, la definizione:

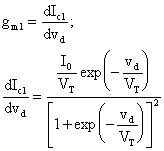
Valutata per V_d=0 ottengo:

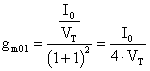
Analogamente per I_C2:

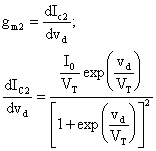
Valutandola per V_d=0 ottengo:

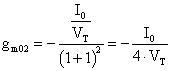
Notando che g_m02 = - g_m01 definisco:

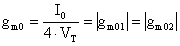
ovvero

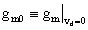
Ora possiamo calcolare le equazioni delle tangenti alle curve I_E1 e I_E2, chiamandole T_E1 e T_E2, nel punto di ascissa 0. Esse saranno:

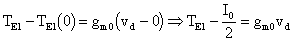
ovvero: ;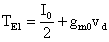

considerando, come è mostrato dalla figura precedente, che fra -V_T e +V_T, si possono confondere le curve con le rispettive tangenti e ricordando, inoltre, che, essendo h_FE » 1, I_C @ I_E possiamo scrivere:

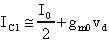
Similmente per T_E2:

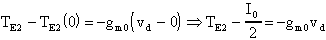
ovvero:

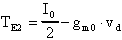
Quindi:

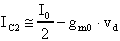
Può essere opportuno, a questo punto, aprire una piccola noticina che, procedendo per altra via, ci condurrà ai risultati appena raggiunti, infatti, se consideriamo i tratti di transcaratteristiche compresi fra -V_T e +V_T, vediamo come sia possibile confonderli con le tangenti alle curve nel punto di ascissa nulla, come ben illustrato nella figura.

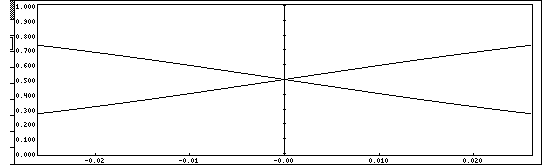
Possiamo, quindi, valutare la transconduttanza, dI_E/dV_T, calcolando la pendenza di tali rette. In altri termini valutiamo i coefficienti angolari delle rette passanti per i punti di ascissa -V_T e +V_T e di ordinate I_E1 (-V_T,+V_T) e I_E2 (-V_T,+V_T).

I_E1 in -V_T vale:

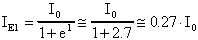
I_E1 in +V_T vale:

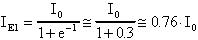
Il coefficiente angolare di questa retta vale:

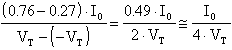
Analogamente per I_E2:

I_E2 in -V_T vale:

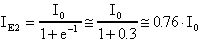
I_E2 in +V_T vale:

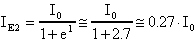
Il coefficiente angolare di questa retta vale:

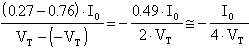
Definendo la quantità: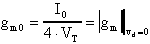

posso ripercorrere quanto visto in precedenza, ricavando I_E1 ed I_E2 (e, quindi, I_C1 ed I_C2) ottenendo le medesime relazioni già viste.

Dall'analisi delle formule che forniscono le correnti di collettore, notiamo che l'amplificatore differenziale ad accoppiamento di emettitore è un circuito che ripartisce fra i due transistors la corrente I₀, fornita dal generatore, in funzione del segnale v_d applicato agli ingressi. Questo effetto di partizione della corrente, può essere considerato funzione lineare di v_d solo se v_d < V_T.

Dopo aver esaminato le caratteristiche generali del circuito differenziale, possiamo addentrarci nel calcolo di alcuni parametri elettrici significativi come: l'amplificazione differenziale A_d, l'amplificazione di modo comune A_c, il rapporto di reiezione di modo comune CMRR, la resistenza d'ingresso e la resistenza d'uscita. Consideriamo quindi il circuito di figura e calcoliamone l'amplificazione differenziale Ad.

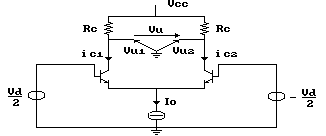
Definiamo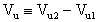 (i morsetti cui è prelevata Vu vengono detti uscita bilanciata, non avendo riferimenti a massa).

Prendendo in considerazione le variazioni, abbiamo:

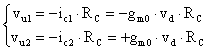
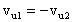
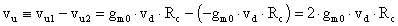
da cui ed ancora:

Posso così ricavare:

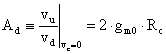
ovvero:

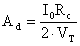
Se ora consideriamo che, per quanto ben fatto, il generatore di corrente I₀ avrà sempre una conduttanza parallelo non nulla (ovvero una resistenza parallelo non infinita), notiamo che una tensione di modo comune, presente sugli ingressi, sarà, in ogni caso, riportata sulle uscite.

Consideriamo infatti il seguente circuito:

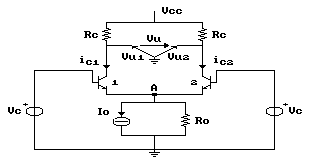
ogni variazione della tensione di modo comune V_c, viene riportata, a meno della V_BE che, in prima approssimazione, si considera costante, ai capi della R₀.

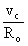
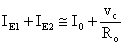
Ciò implica che ogni variazione v_c della V_c, comporta una variazione circa pari a della corrente che scorre in R_o. Facendo l'equazione al nodo A otteniamo:

Essendo I_E1=I_E2, posso dire che:

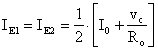
Per le variazioni (I₀ = cost.);

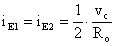
Essendo i_c1 @ i_e1 ed i_c2 @ i_e2 posso ricavare: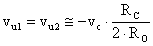

Il guadagno di modo comune (riferito alle uscite 1 e 2) risulta così pari a:

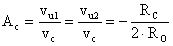
É evidente che se il circuito fosse perfettamente simmetrico (R_C1 = R_C2, i due transistors uguali, etc.) una variazione del modo comune v_c all'ingresso, si tradurrebbe in un'uscita differenziale nulla. Non essendo così nella realtà avremo, oltre ad un segnale pari ad A_cv_c comune sulle uscite sbilanciate, anche un segnale differenziale vu =_/0, come causa di un segnale di modo

mune sugli ingressi.

Volendo ricavare il C.M.R.R., si ottiene:

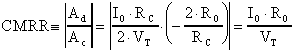
Gli stessi risultati trovati per Ad ed Ac possono essere ricavati sostituendo ai transistors i loro circuiti equivalenti e risolvendo, così, la rete con i metodi convenzionali.

Calcoliamo, ad esempio, il guadagno differenziale A_d del seguente circuito:

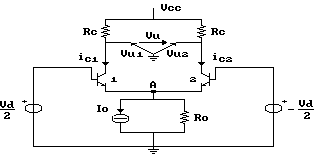
osserviamo che, per le variazioni, il punto A, a causa della simmetria del circuito, è a potenziale costante.

Inoltre, come di consueto, V_CC = cost. A questo punto, nulla vieta, per le variazioni, di considerare il punto A come una massa e di ridisegnare il circuito come nella figura seguente:

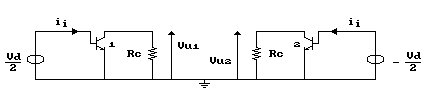
É semplice calcolare:

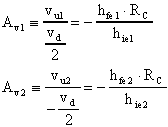
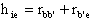
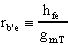
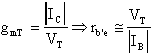
Se i transistors sono uguali ed ugualmente polarizzati, quindi con la stessa I_E, ricordando che , essendo ed essendo , posso dire che le due h_ie sono uguali, e così pure le h_fe.

Pertanto:

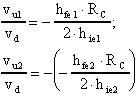
Ricordando che:

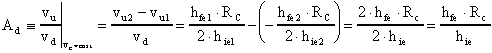
Calcoliamo ora la resistenza d'ingresso differenziale.

, notando che: , otteniamo:

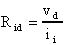
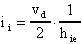
Prendiamo nuovamente in considerazione le relazioni e .

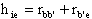
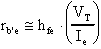
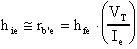
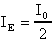
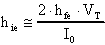
Vediamo che, essendo r_bb' (la Base Spreading Resistance) dell'ordine del centinaio di ohm, se la I_e è piccola r_b'e è dell'ordine delle migliaia di ohm; posso così trascurare r_bb' ed affermare che da cui, ricordando che la I_e a riposo è pari a, sostituendo ottengo:

mettendo a sistema le relazioni testè ricavate, ottengo:

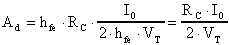
che coincide con la formula già trovata per altra via.

Inoltre, per la R_id, abbiamo:

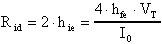
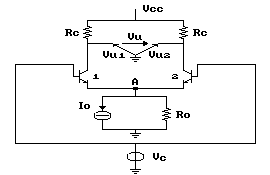
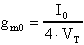
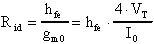
d'altro canto, R_id @ 2·r_db'e (essendo r_b'e@ hie). Considerando il circuito differenziale nel suo insieme, posso considerare una r_db'e dello stadio, questa, come nel caso di un singolo transistor, è uguale a h_fe/g_m0, ricordando che , mettendo a sistema le due relazioni posso dire:

formula identica a quella appena ricavata.

Consideriamo ora il modo comune. Ridisegnamo, a tal fine, il circuito:

Anche in questo caso ci riferiamo alle variazioni, per cui non consideriamo il contributo del generatore I₀, e la V_cc viene posta a massa.

Ora, nell'ipotesi che i due transistors siano uguali ed alla stessa temperatura, avendo la stessa V_BE, avranno anche la stessa corrente di emettitore I_E e, quindi, anche la stessa corrente di collettore I_C; se le resistenze di carico R_c sono uguali, i due collettori saranno equipotenziali, e nulla vieta di cortocircuitarli mettendo le R_c in parallelo. In pratica possiamo considerare tutto lo stadio come un solo transistor, risultato del parallelo fra T₁ e T₂, caricato con una resistenza pari a R_c/2. Il circuito si trasforma come segue:

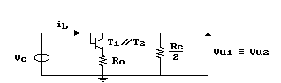
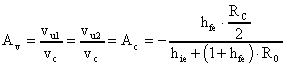
ma se hfe>>1 e hie<<(1+h_fe)R₀ allora:

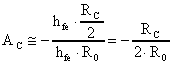
identica alla relazione già calcolata.

Aprendo un piccolo inciso, potevamo dire subito che, approssimativamente, il guadagno in tensione di un transistor connesso ad emettitore comune con resistenza di emettitore, è pari al rapporto fra resistenza di carico e resistenza di emettitore cambiato di segno.

Considerando nuovamente l'amplificazione di modo comune, osserviamo la figura seguente:

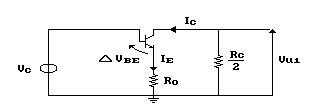
Applichiamo la legge di Kirchoff alla maglia d'ingresso:

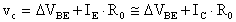
e

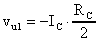
quindi

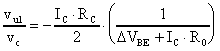
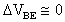
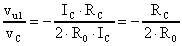
ma per cui:

analoga alla relazione precedentemente trovata.

La resistenza d'ingresso per il modo comune sarà:

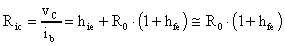
Da qui, possiamo notare che, essendo R₀ la resistenza posta in parallelo ad un generatore di corrente e, pertanto, già di per sè sufficientemente elevata, la resistenza di ingresso per il modo comune dello stadio differenziale, sarà grandissima.

Torna all'indice

La dinamica d'ingresso per il modo comune, come già ricordato, è il campo di valori nel quale può variare un segnale di modo comune senza che intervengano fenomeni di non linearità negli elementi attivi componenti l'amplificatore.

Esaminiamo, ora, nel caso di un differenziale che utilizzi transistors a giunzione, da cosa dipenda.

Osserviamo il circuito in figura:

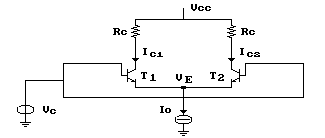
È immediato vedere come il segnale di modo comune, applicato agli ingressi, non possa superare il valore della tensione sui collettori dei transistors, contrariamente si verificherebbe un'inversione di polarità, fra le basi ed i collettori, che porterebbe i transistors stessi alla saturazione.

Quindi, volendo calcolare il limite superiore della dinamica d'ingresso per il modo comune, consideriamo il valore della tensione a riposo V_CO sui collettori di T₁ e T₂, questo valore praticamente non cambia al variare di V_c, in quanto l'amplificazione di modo comune è molto piccola, quindi possiamo scrivere la seguente relazione:

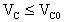
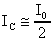
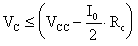
Consideriamo ancora il circuito della figura precedente; la tensione V_CO sarà data dalla differenza fra la tensione di alimentazione V_CC e la tensione ai capi della resistenza R_C. Vediamo, allora, che, considerando la corrente , la disuguaglianza si trasformerà nella seguente:

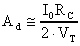
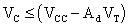
e ricordando che l'amplificazione differenziale è definita come , possiamo scrivere:

Dal risultato ottenuto vediamo che, fissata la tensione di alimentazione V_cc, per ottenere un'alta dinamica superiore d'ingresso possiamo solamente diminuire l'amplificazione differenziale. Per superare questa difficoltà ed ottenere sia un'ampia dinamica superiore sia una elevata amplificazione differenziale, sostituiamo i resistori di carico R_C con un circuito che presenti una bassa resistenza apparente (piccola caduta di tensione ai sui capi) ed una elevatissima resistenza differenziale. Questo circuito, utilizzato nei più recenti circuiti integrati monolitici, è lo "specchio di corrente".

Valutiamo, ora, il limite inferiore per la dinamica di modo comune. Vediamo, considerando ancora la figura precedente, che la tensione V_E sugli emettitori di T₁ e T₂ è pari a V_E = V_C - V_BE.

Il livello di tensione V_E non deve scendere al di sotto del valore che assicura, ancora, un corretto funzionamento per il generatore di corrente I_O. Quindi, affinchè il limite inferiore per la dinamica di modo comune sia il più alto possibile, si rende necessario che, ai capi del generatore di corrente, vi sia una caduta di tensione molto bassa. Tra i generatori di corrente, lo "specchio di corrente" è quello che fa al caso nostro, in quanto la caduta di tensione ai suoi capi è di appena poche centinaia di millivolt.

Utilizzando gli accorgimenti descritti è possibile ottenere una dinamica d'ingresso che si estenda, a meno di qualche centinaio di millivolt, da -V_cc a +V_cc.

Torna all'indice

Consideriamo il seguente circuito:

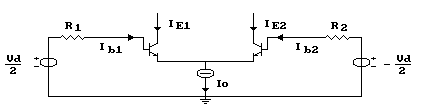
Se il circuito fosse realizzato con componenti ideali, per v_d = 0 si otterrebbe I_C1 = I_C2, come ampiamente già dimostrato.

Siccome il circuito non è ideale per v_d = 0 si ha I_C1 ¹ I_C2, ovvero, si ha un "offset" in uscita.

Quello che ci proponiamo di valutare, è l'offset d'ingresso, ovvero quel particolare valore V_o della tensione v_d che rende .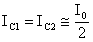

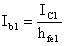
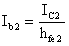
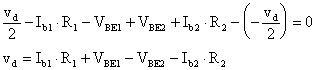
Consideriamo e , supponendo inoltre i transistors alla stessa temperatura, possiamo valutare l'equazione alla maglia:

ma

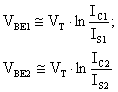
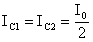
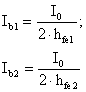
Per valutare V_o devo, come accennato prima, imporre: ; pertanto varranno le seguenti relazioni:

Inoltre possiamo calcolare:

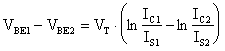
da cui, per quanto imposto precedentemente, ricaviamo:

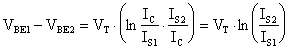
Sostituendo questi risultati nell'espressione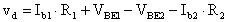

ed inoltre, considerando che il valore di v_d così ottenuto, è il valore di V_o cercato, diciamo che:

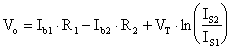
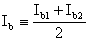
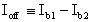
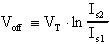
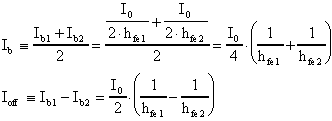
Definendo con la corrente di polarizzazione d'ingresso (Input Bias Current), con l'offset di corrente di ingresso (Input Offset Current) e con l'offset di tensione in ingresso (Input Offset Voltage) e ricordando le espressioni relative alle correnti di base, possiamo scrivere:

Osserviamo subito come i termini I_off e V_off risultino nulli se i due transistors sono identici; questa circostanza sarà oggetto, in seguito, di un'analisi più approfondita.

Riscrivendo l'espressione che mi fornisce V_o come:

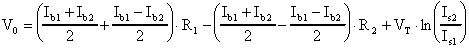
e sostituendovi le definizioni, otteniamo:

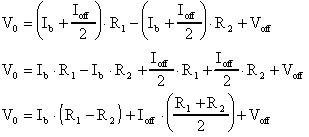
Analizziamo ora l'espressione ottenuta: se R₁ ed R₂ sono le più piccole e le più uguali possibile, il termine in I_b tende a zero, inoltre, se i transistors sono il più possibile simili, come visto in precedenza, anche gli altri due termini dell'ultima espressione andranno a zero; se ne deduce che, sotto queste condizioni ottimali, V_o tenderà a zero.

Da quanto detto risulta chiaro, però, che non potremo sperare di avere un amplificatore differenziale in cui la V_off sia nulla, ma dovremo pensare ad un circuito, che compensi gli effetti inevitabili degli offsets.

Pensiamo così di poter recuperare gli offsets sacrificando un ingresso del circuito per introdurre, per suo tramite, la tensione di compensazione. La rete deve essere costruita in modo tale da presentare una resistenza equivalente il più possibile uguale alla resistenza che il circuito "vede" dall'altro ingresso.

Realizziamo così il seguente circuito:

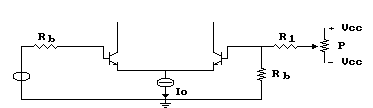
Chiaramente, dovrà essere R₁>>R_b in modo che, variando P, non vari in maniera sensibile la resistenza "vista" dall'ingresso, inoltre, perchè possa essere recuperato, l'offset massimo in ingresso dovrà essere

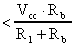
Se non volessimo sacrificare un ingresso, potremmo pensare di distribuire diversamente la corrente I_O, ad esempio ponendo un piccolo potenziometro fra i due emettitori.

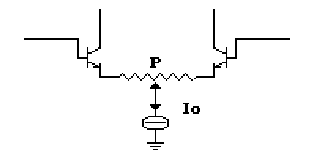
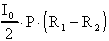
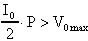
Considerando il potenziometro come somma di due resistenze: P = R₁+R₂,notiamo che si introduce nella maglia d'ingresso una tensione che può annullare l'offset in ingresso V_o. In questo caso dovrà essere verificata la relazione:

L'introduzione del potenziometro, però, fa diminuire l'amplificazione differenziale in quanto aumenta la resistenza degli emettitori. Posso, pertanto, pensare di "dosare" la I_C, anziché la I_O, ponendo il potenziometro fra i due collettori. Realizziamo perciò il seguente circuito:

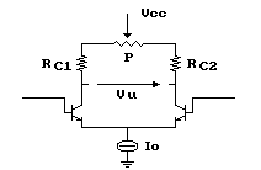
In questo caso, al variare di P, variano R_C1 e R_C2 cosicchè, pur conc correnti I_C1 ¹ I_C2, possiamo ottenere ugualmente I_C1·R_C1 = I_C2·R_C2, ovvero, in ultima analisi, avremo recuperato gli offset garantendo una tensione V_u = 0.

Riunendo, ora, tutto quanto visto in un unico circuito, potremo realizzare lo stadio d'ingresso di un buon amplificatore per continua come rappresentato nella figura seguente:

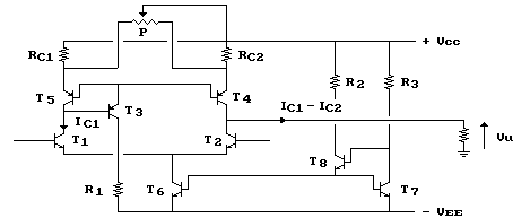
Come vedremo, a questo schema di massima vanno aggiunti uno stadio di amplificazione intermedio ed uno stadio finale, le cui caratteristiche saranno analizzate in separata sede.

Osservando il circuito, si noterà senz'altro la presenza di uno specchio di corrente, realizzato con transistors di tipo p-n-p, posti sui collettori dello stadio differenziale. La corrente che fluisce nel collettore di T₄ ripete fedelmente la corrente I_C1, per cui sul morsetto d'uscita sarà presente la corrente I_C1 - I_C2, proporzionale, per quanto visto, alla tensione V_d.

Vediamo, inoltre, come sia stato inserito, fra gli emettitori dello specchio di corrente, un potenziometro per il recupero degli offsets. Ricordando che le resistenze, poste sugli emettitori dello "specchio di corrente", fanno sì che le correnti dei collettori non siano "speculari", ma bensì proporzionali al logaritmo del loro rapporto, si comprende come, variando il rapporto di partizione, varino di conseguenza I_C1 ed I_C2, ottenendo così il desiderato recupero degli offsets.

Ancora, possiamo notare la scelta dello "specchio di corrente" come generatore di corrente continua per i transistors T₁ e T₂ ed, infine, l'uso di un'alimentazione duale per il circuito.

Torna all'indice

Possiamo, a questo punto, introdurre le specifiche a cui deve, generalmente, soddisfare un amplificatore per grandezze continue esaminandole una per una. Esse sono:

1) Piccole derive termiche

Il maggior responsabile delle derive termiche è il primo stadio, quindi dovrà essere un amplificatore differenziale il più simmetrico possibile; inoltre si vorranno avere bassi valori di I_b e I_off ma, come visto in precedenza:

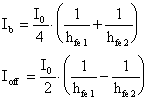
quindi, per soddisfare questa ulteriore richiesta occorrerà polarizzare i transistors con una piccola I_O.

Se il primo stadio presenta un'amplificazione elevata, superiore a diverse centinaia, le derive e gli offsets degli stadi successivi hanno poca importanza, in quanto esse vengono riportate all'ingresso divise per l'amplificazione del primo stadio. Se ciò non dovesse verificarsi, anche il secondo stadio dovrà essere differenziale per evitare che la sua deriva termica, riportata all'ingresso, sia comparabile o, peggio ancora, superiore a quella del primo stadio.

2) Elevata dinamica d'ingresso per il modo comune

La dinamica d'ingresso per il modo comune dipende dal primo stadio; per renderla massima occorre agire sia sulle resistenze di carico dei collettori, sia sul generatore di corrente I_O. I carichi sui collettori devono sì presentare una bassa resistenza apparente (piccola caduta di tensione continua ai loro capi), ma un'elevatissima resistenza differenziale, è quindi opportuno sostituire alle resistenze lo specchio di corrente). Il generatore di corrente deve essere scelto in modo che richieda, per funzionare, una piccola caduta di tensione ai suoi capi, quindi la scelta cadrà ancora sullo specchio di corrente.

3) Bassa cifra di rumore

La possibilità di generare rumore è legata alla struttura stessa del transistor; in più, il rumore dipende dalla polarizzazione del componente. Senza approfondire ulteriormente l'argomento, è bene ricordare che i costruttori riportano, nei Data Sheets, la corrente di collettore a cui si ha la minima cifra di rumore. Quindi, per ottenere una bassa cifra di rumore, occorrerà polarizzare i transistors con valori di corrente di collettore vicini a quello dato. In genere questo valore è molto piccolo, dell'ordine della decina di mA, quindi anche la corrente I_O dovrà essere molto piccola. Considerando che il rumore è generato principalmente dal circuito con maggior amplificazione, bisognerà curare particolarmente la polarizzazione del primo stadio.

4) Elevata impedenza differenziale d'ingresso

Per avere un'alta impedenza differenziale d'ingresso, ricordando che 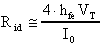, occorrerà, una volta in più, imporre una piccola corrente I_O.

5) Minima amplificazione di modo comune (cioè massima CMRR)

L'amplificazione di modo comune A_C dipende essenzialmente dal primo stadio, occorre, quindi, che esso sia il più simmetrico possibile; inoltre, dato che 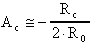,per ottenere un basso valore dell'amplificazione di modo comune, dovrà essere usata particolare attenzione nella progettazione del generatore di corrente I_O.

6) Elevata impedenza d'ingresso per il modo comune

Per avere alta impedenza d'ingresso per il modo comune, occorre realizzare al meglio il generatore di corrente continua che alimenta gli emettitori dei transistors del differenziale in quanto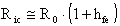

7) Elevata amplificazione differenziale

In un amplificatore per grandezze continue, l'amplificazione globale è il prodotto delle amplificazioni dei singoli stadi che lo costituiscono. É però opportuno, onde evitare il più possibile l'influenza di offsets, di derive e del rumore degli stadi successivi, che il primo stadio abbia, da solo, una amplificazione molto più elevata degli altri. Dato che ciò è ottenuto rendendo grande il prodotto , per non diminuire la dinamica d'ingresso aumentando il valore delle resistenze di collettore R_C, sarà opportuno sostituire il carico resistivo con uno specchio di corrente che ha il pregio di unire ad un'alta resistenza differenziale una bassa resistenza apparente.

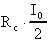
8) Elevata velocità ovvero elevata "Slew-rate"

Per costituzione intrinseca del transistor, non possiamo prescindere dalle capacità parassite, che danno fastidio riducendo la velocità di risposta dell'elemento attivo. Ora, la velocità di variazione della tensione d'uscita è data, come per la più usuale velocità ds/dt, dalla variazione di V_u al variare del tempo. In formule: essendo SR la Slew rate. Dalla fisica sappiamo che , indicando con C la capacità del condensatore considerato. Visto che in un circuito differenziale la massima corrente che può circolare in un transistor è pari a I_O (questo nell'ipotesi che l'altro transistor sia interdetto) vediamo che . Questo significa che per avere un'elevata Slew Rate occorre avere una corrente di polarizzazione il più alta possibile, contrariamente a tutte le altre esigenze finora considerate. Per fortuna ci viene in aiuto la tecnologia che ci propone da una parte i FET, con corrente di gate praticamente nulla ( è la corrente di saturazione inversa della giunzione gate-source) e svincolata dalla corrente I_O ed elevatissima impedenza d'ingresso, dall'altra i cosiddetti transistors "superbeta" che hanno un b elevatissimo, dell'ordine delle migliaia. Con l'uso dei FET si riescono ad ottenere velocità d'uscita dell'ordine delle migliaia di Volt al microsecondo.

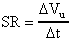
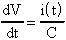
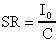
9) Bassa impedenza d'uscita

Il compito di fornire una bassa impedenza d'uscita sarà svolto essenzialmente dallo stadio finale.

10) Tensione nominale d'uscita di 0 V

Si ottiene una tensione nominale d'uscita di 0 V, con ingressi a massa, dimensionando opportunamente gli stadi successivi al primo, in modo da realizzare il necessario scalamento dei livelli di tensione. Agli stadi successivi al primo è affidato anche il compito di aumentare l'amplificazione globale.

11) Elevata dinamica d'uscita

L'elevata dinamica d'uscita, che dipende essenzialmente dallo stadio finale, è funzione della resistenza di carico. Occorre, tuttavia, controllare che gli stadi precedenti rimangano in linearità per tutta l'escursione di tensione consentita al segnale d'uscita.

12) Elevato rendimento di potenza

Anche il rendimento di potenza dell'amplificatore, definito come il rapporto fra la potenza fornita al carico e quella assorbita dall'alimentazione, dipende soprattutto dalla cura con cui è stato progettato l'ultimo stadio.

Torna all'indice

Come già accennato gli amplificatori per grandezze continue sono composti da più di uno stadio. Avendo già analizzato in dettaglio lo stadio iniziale, esaminiamo ora quello intermedio.

Scopi principali dello stadio intermedio sono contribuire all'incremento del guadagno di tensione totale dell'amplificatore senza peggiorare slew rate e derive, adattare l'impedenza d'uscita dello stadio d'ingresso con l'impedenza d'ingresso dello stadio finale ed effettuare lo scalamento in tensione per poter avere uscita nulla quando gli ingressi siano cortocircuitati.

Per questo stadio si possono utilizzare sia l'amplificatore differenziale che circuiti a singolo transistor, la scelta fra i due tipi di soluzione si basa soprattutto sulla necessità di mantenere alto il rapporto di reiezione di modo comune (CMRR) e di minimizzare gli effetti che il circuito stesso pone presentandosi come carico, in continua, per lo stadio precedente.

Come abbiamo visto il CMRR è imposto dallo stadio differenziale d'ingresso. Quindi la realizzazione dello stadio intermedio con circuiterie non differenziali, cioè a singolo transistor, non potrà influenzare, e quindi migliorare, il CMRR totale. Questo tipo di considerazione, ci fa protendere verso l'uso, per questo stadio, di un amplificatore differenziale. Bisogna, però, tener presente che circuiti di questo tipo generano, se non ben bilanciati, delle tensioni di offset che vengono interpretate come segnali differenziali dagli stadi successivi. Di ciò, e degli effetti di carico introdotti, bisognerà tenere in doveroso conto, ricorrendo, per la sua realizzazione, alle tecniche di minimizzazione degli offsets che abbiamo visto nel dettaglio in precedenza.

Normalmente la scelta cade o su due stadi differenziali di moderato guadagno, oppure su uno stadio differenziale ad alto guadagno seguito da uno stadio formato da un singolo transistor.

In conclusione le soluzioni maggiormente adottate per lo stadio intermedio sono: differenziali a transistors bipolari o a FETs, amplificatori ad emettitore comune, ovvero suorce comune, ed emitter follower, ovvero source follower. Ognuno dei circuiti qui elencati provvede allo scalamento del livello di tensione, come è rappresentato dalle illustrazioni seguenti:

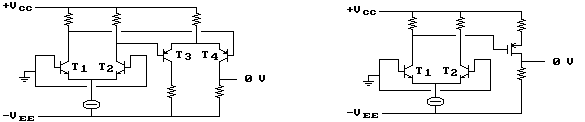
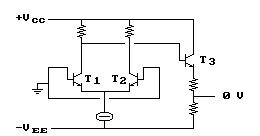
Per lo stadio differenziale lo spostamento del livello è ottenuto usando transistors di tipo PNP, in questo modo la necessaria caduta di tensione è dovuta alla differenza di potenziale fra collettore e base dei transistors T₃ e T₄.

Una situazione analoga si presenta per lo stadio a source comune, dove lo scalamento è dovuto alla tensione di polarizzazione fra gate e drain.

Nell'emitter follower lo slittamento del livello è ottenuto tramite un partitore di tensione. Occorre, però, specificare che l'uso di questo artificio riduce il guadagno di tensione; per ovviare all'inconveniente si possono utilizzare diverse soluzioni, alcune delle quali sono riportate nella figura seguente:

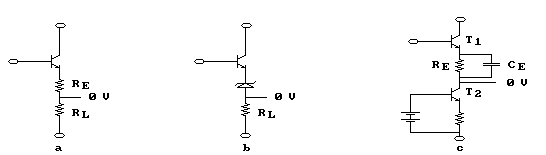
L'impedenza del diodo zener della seconda immagine è piccola in confronto ad R_L, quindi, in questo modo, si riesce a limitare la perdita di guadagno; tuttavia il rumore introdotto dallo zener può peggiorare le prestazioni dell'amplificatore. In alternativa si può modificare il partitore di tensione inserendo, al posto della resistenza di carico R_L, un pozzo di corrente che, notoriamente, presenta resistenza d'uscita molto alta, ottenendo, così, il circuito di fig. c. Il condensatore C_E è stato inserito per compensare l'effetto della capacità di giunzione vista dal collettore di T₂, che alle alte frequenze cortocircuiterà la resistenza d'uscita del generatore di corrente.

Esaminiamo, ora, in dettaglio, uno stadio intermedio ad emitter follower. Chiaramente i risultati ottenuti varranno, con le ovvie modifiche, per ognuno dei circuiti riportati in figura.

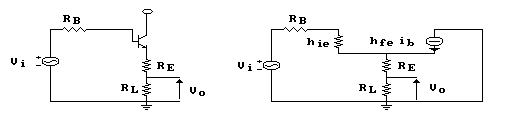
Ricordiamo qui di seguito solo le formule principali, dato che il circuito sarà sicuramente noto al lettore. Nel ricavare queste espressioni abbiamo trascurato i parametri h_oe ed h_re e li trascureremo anche nella restante parte della trattazione.

Il guadagno di tensione totale sarà:

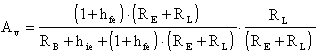
É da notare come il partitore di tensione d'uscita riduca il guadagno di tensione che, come noto, per questo circuito è già minore di uno.

La resistenza d'ingresso è data da:

)

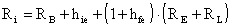La resistenza d'uscita sarà uguale a:

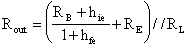
Notiamo che aumentando R_L si può migliorare il rapporto di partizione d'uscita, migliorando, di conseguenza, il guadagno di tensione, ma la resistenza d'uscita avrà un valore comunque basso, sempre più prossimo ad R_E mano a mano che R_L aumenterà.

Il guadagno di corrente è espresso dalla relazione:

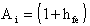
Vediamo qui di seguito, uno stadio intermedio ad emettitore comune:

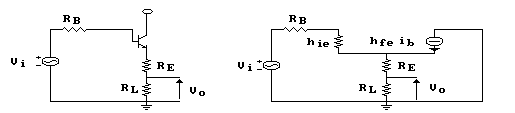
Anche di questo circuito forniremo solo le formule principali, essendo, sicuramente, noto.

Il guadagno di tensione è:

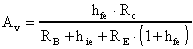
La resistenza d'ingresso è fornita da:

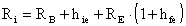
La resistenza d'uscita sarà espressa come:

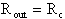
Il guadagno di corrente risulta:

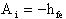
Se desiderassimo migliorare il guadagno di tensione di questo circuito potremmo utilizzare, al posto della resistenza di carico R_C, un pozzo di corrente, ottenendo lo schema riportato infigura:

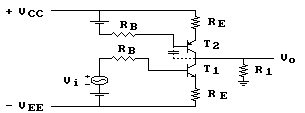
La resistenza dinamica d'uscita del pozzo di corrente è notoriamente alta e si comporta come una resistenza dicarico di valore elevato. Il guadagno, proporzionale alla resistenza di collettore, risulta così aumentato.

Tenendo però presente il valore relativamente basso della resistenza differenziale del circuito stesso, fra i collettori ed il morsetto positivo dell'alimentazione non si avrà più quella forte caduta di tensione che avrebbe avuto luogo utilizzando una resistenza di pari valore, così facendo abbiamo migliorato anche la dinamica d'uscita.

Gli svantaggi che, purtroppo, accompagnano l'uso di tale stratagemma, sono legati a problemi di riduzione della banda passante e della resistenza d'ingresso, che si vorrebbe alta per non permettere fenomeni di partizione di tensione con lo stadio precedente. Consideriamo la figura precedente; in essa è rappresentata la capacità di giunzione fra base e collettore che si pone in parallelo alla resistenza d'uscita del generatore di corrente. Quindi sul collettore di T₁, al posto della resistenza R_C, dovremo considerare l'impedenza Z_C che, inserendo un polo a frequenze relativamente basse, ha l'effetto di ridurre la banda passante.

Torna all'indice

Come è già stato evidenziato, allo stadio finale è assegnato il compito di presentare:

1) Bassa impedenza d'uscita

2) Elevata dinamica per il segnale in uscita

3) Elevato rendimento di potenza.

Esaminiamo queste tre specifiche: per rendere bassa la resistenza d'uscita possiamo utilizzare un transistor a collettore comune però, affinchè il segnale venga riprodotto fedelmente, ovvero con la minor distorsione possibile, occorre che l'amplificatore funzioni in classe A.

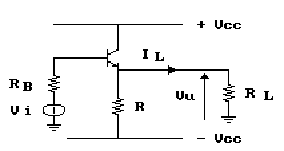
Si dice che un amplificatore funziona in classe A quando la corrente I_L è fornita al carico per l'intero periodo del segnale, supposto sinusoidale, ovvero per un angolo q_C di conduzione pari a 2p. Perchè‚ questo sia possibile bisogna polarizzare il transistor al centro della zona lineare delle caratteristiche, preoccupandoci che il punto di funzionamento non vada ad interessare, nella sua escursione, zone di non linearità (saturazione ed interdizione); ma ciò comporta la necessità di imporre correnti di emettitore abbastanza elevate. Quindi, anche in assenza di segnale, viene assorbita dall'alimentazione una potenza non trascurabile; questa circostanza limita pesantemente il rendimento di potenza del circuito.

Per aggirare il problema possiamo considerare l'ipotesi di utilizzare amplificatori in classe B. Si dice che un amplificatore funziona in classe B se, in corrispondenza di un'eccitazione sinusoidale, il carico è percorso da corrente solo per metà periodo.

Possiamo quindi realizzare lo stadio finale utilizzando una coppia di transistor complementari, cioè NPN e PNP, in configurazione push-pull come mostrato in figura, dove con il generatore V_i e con la resistenza R_B si è voluto indicare l'equivalente Thevenin degli stadi precedenti.

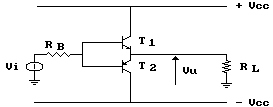
Se la tensione d'ingresso è positiva e superiore alla tensione di soglia V_S del transistor (V_S = 0,6 per il silicio e V_S = 0,2 per il germanio) sarà in conduzione il transistor NPN T₁, mentre T₂ sarà interdetto; se, al contrario, V_i è negativa ed in valore assoluto maggiore di V_S condurrà il transistor PNP T₂, mentre T₁ sarà interdetto. Ogni transistor, quando è in conduzione, si comporta come un normale stadio a collettore comune, trasferendo tutta la corrente che lo percorre al carico.

La potenza apparente è data dal prodotto dei valori efficaci della tensione e della corrente.

Come noto, la definizione di valore efficace di una grandezza periodica x(t) di periodo T è data da:

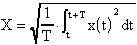
Questa relazione, come noto, si riduce, nel caso di x(t) sinusoidale, al rapporto fra il suo valore massimo X_m e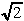

Pertanto, un amplificatore in classe B in configurazione push-pull, in presenza del segnale d'ingresso, cederà al carico la potenza P_L data dalla relazione:

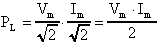
dove I_m e V_m sono i valori di picco, rispettivamente, della corrente e della tensione.

La corrente che il collettore di ogni transistor sotto carico assorbe dall'alimentazione, è data dal valor medio del segnale sinusoidale d'ingresso calcolato sul semiperiodo, pertanto sarà pari a:

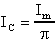
Quindi i transistor assorbiranno dall'alimentazione la potenza P_A pari a:

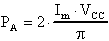
Il fattore 2 in questa formula si deve al fatto che il sistema è composto da due transistor.

Il rendimento h del circuito, calcolato come il rapporto fra la potenza P_L ceduta al carico e la potenza P_A assorbita dall'alimentazione, viene quindi ad essere espresso dalla relazione:

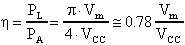
Ritenendo trascurabile la tensione fra collettore ed emettitore del transistor, possiamo considerare V_m@V_CC. In questo caso il rendimento è massimo e risulta pari circa a 0,78. Il risultato raggiunto, confrontato con quello di un amplificatore in classe A pari a circa 0.25, giustifica la scelta di un sistema push-pull in classe B per lo stadio finale.

Il fatto che i transistor conducano solo quando la tensione fra base ed emettitore V_BE supera il valore di soglia V_S, comporta che vi sia una fascia di tensione, intorno al valore di 0 Volt, in cui entrambi i transistor sono interdetti. In questo modo la forma d'onda del segnale d'uscita presenterà una distorsione, detta di "cross-over", o di "attraversamento", che è riportata nella figura seguente.

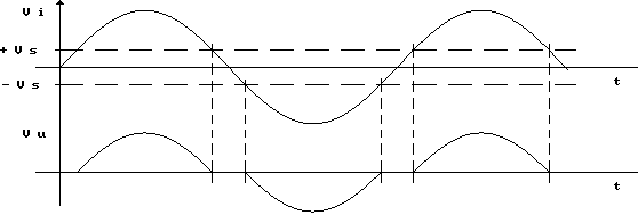
Per eliminare questo inconveniente possiamo dare alle basi dei transistor una caduta di potenziale tale da compensare le tensioni di soglia V_S e realizzare il circuito rappresentato in figura.

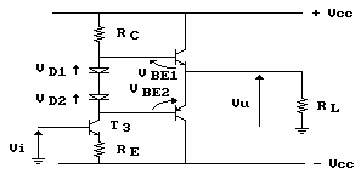
I diodi polarizzati direttamente conducono avendo ai loro capi una caduta di tensione pari a V_D, circa uguale alla tensione di soglia V_S dei transistor. Le tensioni V_D e V_BE, come mostra la figura, si sommano algebricamente con l'effetto di compensare le tensioni di soglia e permettere ai transistor di condurre per qualunque valore di tensione del segnale d'ingresso.

La soluzione circuitale adottata ci permette, quindi, di riprodurre all'uscita un segnale privo della distorsione di cross-over.

È da notare inoltre che le derive termiche delle tensioni sui diodi sono circa uguali a quelle dei transistor, quindi il sistema risulta largamente indipendente dalla temperatura.

Nel circuito visto, il transistor T₃, connesso ad emettitore comune, costituisce lo stadio pilota.

Lo stadio finale deve anche essere protetto da cortocircuiti accidentali sia verso massa sia verso le alimentazioni. A questo scopo possiamo inserire sugli emettitori dei transistor delle resistenze di protezione come mostrato nella figura seguente.

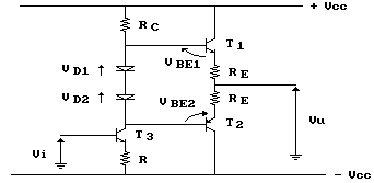
Le resistenze R_E permettono ai transistor di dissipare, senza danni, l'elevata potenza che interviene in caso di cortocircuito.

Infatti, la potenza dissipata da ogni transistor è data da:

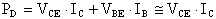
Nel caso in cui l'uscita venga accidentalmente cortocircuitata a massa, risolvendo l'equazione alla corrispondente maglia, possiamo scrivere:

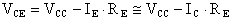
da cui, sostituendo nella relazione precedente, ricaviamo:

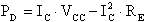
Questa relazione rappresenta una parabola con concavità rivolta verso il basso e, pertanto, presenta un massimo in corrispondenza del vertice.

Dalla geometria analitica possiamo immediatamente ricavarne le coordinate pari a:

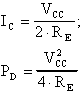
L'ordinata del vertice rappresenta la potenza massima dissipata dal transistor, che dovrà essere inferiore alla potenza massima dissipabile, P_max, alla massima temperatura prevista per il suo funzionamento. Allora possiamo scrivere:

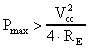
quindi:

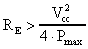
Le resistenze R_E si trovano in serie al segnale d'uscita, pertanto aumentano la resistenza d'uscita dello stadio finale e, tramite la caduta su di esse, provocano una diminuzione della dinamica. Dobbiamo valutare, però, un altro effetto dovuto alla presenza delle resistenze d'emettitore. Supponiamo che sia V_U>0, cosa che si verifica quando il segnale di ingresso è tale da mandare in conduzione il transistor T₁. T₂, in questa circostanza, dovrebbe essere interdetto, quindi la V_BE2 deve essere minore della sua V_S. V_BE2, però, è, dall'equazione alla maglia interna, pari a:

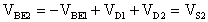
Se questa tensione, a causa delle inevitabili tolleranze sulle varie giunzioni, fosse maggiore di V_S2, il transistor T₂ sarebbe già in conduzione e non al limite dell'interdizione. Ciò significa che, per il tempo necessario al segnale per attraversare l'intorno di 0 V (+ V_S), entrambi i transistor sono in conduzione, quindi assorbono corrente, abbassando, in tal modo, il rendimento totale.

Inserendo le resistenze d'emettitore il bilancio della maglia diviene:

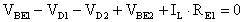
da cui ricaviamo:

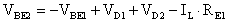
Questa relazione differisce dalla precedente per il termine di contropolarizzazione I_L R_E1 che porterà V_BE2 ad essere sicuramente minore di V_S2 garantendo, quindi, l'interdizione del transistor e migliorando il rendimento globale dell'amplificatore.

L'incremento della resistenza d'uscita e la diminuzione della dinamica, introdotte da questa protezione, potrebbero, però, risultare inaccettabili. Per ridurre il valore della resistenza di emettitore, possiamo o ricorrere all'uso di un dissipatore di calore, per permettere ai transistor di dissipare maggior potenza, o ricorrere all'uso di appositi circuiti di protezione. Un esempio in tal senso è costituito dal circuito illustrato in figura .

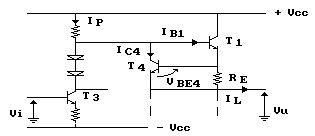
Questo tipo di protezione viene definito "protezione attiva". L'azione di questo circuito si può spiegare in questo modo: il transistor T₄ non entra in conduzione fino a quando la sua V_BE non supera la soglia V_S, in questo caso, dall'analisi del circuito, risulta che V_BE4 = R_E·IL. Quindi occorre dimensionare la resistenza R_E in modo tale che la caduta di tensione ai suoi capi superi la soglia V_S solo quando la corrente sul carico raggiunge un valore limite fissato I_max superato il quale T₄ entra in conduzione sottraendo la corrente I_C4 dalla base di T₁, inoltre ogni aumento della corrente I_L provoca un incremento della tensione V_BE4, con conseguente aumento della corrente di collettore I_C4, che limita ulteriormente la corrente di base I_B1. Infatti:

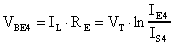
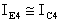
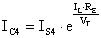
quindi, essendo possiamo asserire che

Essendo 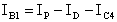, si nota come, all'aumento di I_L, aumenti anche I_C4 e, quindi, diminuisca I_B1 facendo diminuire la stessa I_L.

In ultima analisi il circuito formato dai due transistors, T₁ e T₄, è un sistema reazionato negativamente in grado di controllare e limitare la corrente d'uscita dell'amplificatore.

Il valore massimo della corrente sul carico I_max è dato dalla seguente relazione:

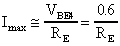
Da questa relazione si nota come la dinamica d'uscita venga diminuita, a causa del circuito di protezione, al massimo di 1.2V, inoltre la resistenza d'emettitore, necessaria per limitare la corrente, ha un valore modesto che aumenta di poco la resistenza d'uscita dell'amplificatore.

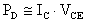
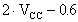
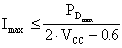
Bisogna osservare che, essendo , bisognerà tenere in conto eventuali cortocircuiti anche fra l'uscita ed il negativo dell'alimentazione che possono portare la V_CE ad un valore pari a . La I_max sarà pertanto fornita dalla relazione:

Una simile soluzione circuitale, purtroppo, può essere utilizzata solo per la massima corrente positiva d'uscita. Se utilizzassimo il circuito riportato nella figura seguente e se si verificasse un cortocircuito accidentale fra uscita e massa, o peggio, col positivo dell'alimentazione, T₃ dovrebbe sopportare una corrente di collettore decisamente elevata.

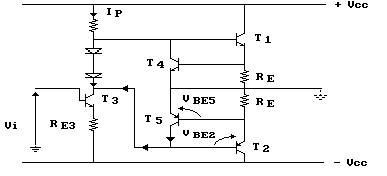
Vediamo, infatti, che se l'uscita viene connessa direttamente a massa lo è anche l'emettitore di T₅ che, a meno delle cadute di tensione V_BE5 e V_BE2, porta a potenziale di massa il collettore di T₃. In questa situazione tutta la tensione di alimentazione -V_CC verrebbe a trovarsi su T₂ ed R_E3. A questo proposito consideriamo l'equazione alla maglia formata dai transistor T₃, T₄ e T₅ con l'uscita cortocircuitata a massa, avremo:

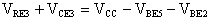
da questa relazione otteniamo:

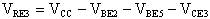
Ricaviamo, ora, la corrente di collettore del transistor T₃, questa sarà, come noto, circa uguale alla corrente di emettitore dello stesso transistor quindi posso scrivere:

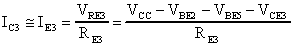
Se la potenza massima dissipabile dal transistor, P_Dmax, è maggiore della potenza 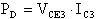, dove la I_C3 è fornita dalla relazione poc'anzi vista, le protezioni introdotte nel circuito della figura precedente garantiscono il corretto funzionamento del dispositivo. In caso contrario occorre dissipare potenza tramite un dissipatore di calore.

Supponiamo, ora, di creare un cortocircuito fra l'uscita ed il positivo dell'alimentazione, avremo la situazione illustrata nella figura a seguire:

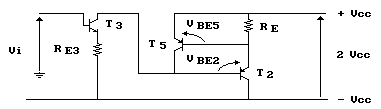
Considerando l'equazione alla maglia possiamo scrivere:

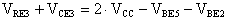
ricavando V_RE3 otteniamo:

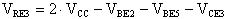
inoltre considerando che I_E3 @I_C3 vale la seguente relazione:

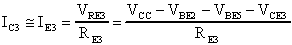
Ancora una volta se la potenza massima dissipabile dal transistor è superiore alla potenza che occorre dissipare, la soluzione circuitale adottata in figura ci assicura il corretto funzionamento dell'amplificatore; qualora ciò non si verifichi bisogna dissipare la potenza in eccesso tramite un dissipatore di calore.

Allo scopo di non sovraccaricare il pilota possiamo cambiare tipo di protezione e realizzare il circuito di seguito illustrato.

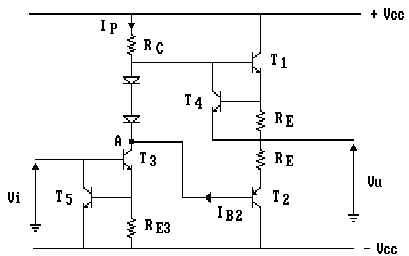
Ad una prima analisi, questo circuito offre una buona protezione attiva; infatti un aumento della corrente di emettitore di T₂ comporta l'incremento della I_B2 e di conseguenza della I_C3. Ma ad una corrente elevata nel transistor pilota, consegue una tensione ai capi di R_E3 tale da portare in conduzione T₅ che, sottraendo corrente alla base di T₃, lo porta verso l'interdizione senza, però, spegnerlo.

Facciamo, ora, alcune considerazioni sulle correnti nei transistor T₂ e T₃. Dobbiamo fare in modo che la corrente I_C3 non sia superiore sia a 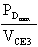che a I_C3max. Occorre, inoltre, che anche il transistor T₂, al limite superiore della dinamica, non sia attraversato da una corrente eccessiva.

Tenendo presente che, in queste condizioni, T₁ è interdetto la legge di Kirchoff, applicata al nodo A, ci permette di scrivere:

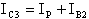
Per abbassare la corrente I_B2 posso, allora, agire solo su I_C3 a patto che sia costante la I_P. Per poter ottenere una corrente costante, penso allora di sostituire la resistenza R_C con un generatore di corrente o, meglio ancora, con uno specchio di corrente:

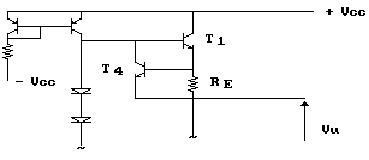
La corrente I_B2 è legata alla corrente d'uscita dalla relazione:

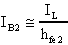
che sostituita nella equazione vista prima fornisce:

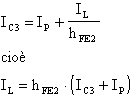
Quindi, limitando la corrente di collettore del transistor pilota (I_C3), sarei in grado di limitare la massima corrente d'uscita, ma il termine h_FE varia in funzione della corrente di collettore I_C2 @ I_L, pertanto l'aver utilizzato il transistor T₅ in reazione al T₃ riesce, sicuramente, a limitare la corrente in quest'ultimo, ma non può garantire la protezione del transistor finale. Per ovviare a questo inconveniente posso inserire un transistor sull'emettitore di T₂ secondo lo schema della figura .

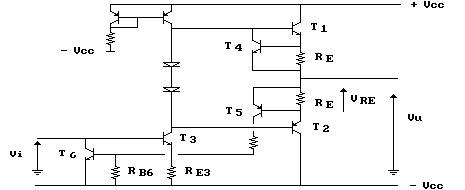
Con questo circuito la corrente I_E2 comanda direttamente il transistor T₅ che entra in conduzione allorchè‚ la tensione V_RE diviene maggiore di 0.6 V. Ora, la corrente di collettore di T₅ fluisce in R_B6 e, non appena la caduta ai suoi capi raggiunge e supera la tensione di soglia (0.6V circa) del transistor T₆, porta questi in conduzione, facendo sì che la sua corrente di collettore riduca la corrente di base di T₃ diminuendo I_C3 e, quindi, I_B2. Pertanto il controllo della corrente d'uscita risulta indipendente dal termine h_FE2 rendendo più affidabile l'effetto protettivo.

Torna all'indice

Torna alla Home Page