La modulazione è un processo che consiste nel traslare l'allocazione in frequenza della banda finita di un segnale informativo. Di fatto, la modulazione è l'alterazione sistematica di una forma d'onda, chiamata portante, secondo le caratteristiche di un'altra forma d'onda: la modulante, ovvero il messaggio.

I motivi per cui si rende necessario modulare un segnale per trasportare informazione sono almeno di quattro fattori:

Assegnazione di bande, cioè ripartizione delle medesime risorse fra più utenti che necessitano di comunicare nello stesso tempo e nello stesso luogo

Agevolare l'irradiazione, cioè meglio adattare il segnale al mezzo trasmissivo

Trasmettere contemporaneamente più segnali differenti, basti pensare alla televisione

Riduzione del rumore e delle interferenze.

Possiamo così schematizzare un canale di trasmissione:

image: 0_home_maurizio_telecomunicazioni_modulazione_modello_di_canale.jpg

In questo modello H

_{T}

(f), H

_{c}

(f) ed H

_{R}

(f) sono le funzioni di trasferimento dei rispettivi blocchi. Generalmente si suppone che il canale sia lineare ed il rumore sia additivo. Mentre, per quanto riguarda i filtri di trasmissione e di ricezione, che dovrebbero essere sempre presenti, si assume che siano filtri passabanda centrati attorno alla frequenza di riferimento della portante f

_{0}

. Se f

_{0}

= 0, i filtri sono dei passabasso e la trasmissione si dice in banda base. In questo ultimo caso, utilizzato, ad esempio, per le comunicazioni fra due calcolatori via seriale o parallela, non vi è modulazione.

Le modulazioni possono essere divise in due grosse branche: analogiche e digitali. A loro volta, in base alle caratteristiche della modulazione stessa, verranno suddivise in altre tipologie.

Prima di procedere all'esame dei vari tipi di modulazione analogica è, però, opportuno richiamare alcune notazioni di base.

Un segnale sinusoidale s(t) può essere rappresentato in forma complessa:

s (t) = a (t) + j b (t) = A (t) e^{j Φ (t)}

in cui:

A (t) = \sqrt{a {(t)}^{2} + b {(t)}^{2}}

prende il nome di inviluppo

Φ (t) = t g^{- 1} (\frac{b (t)}{a (t)})

prende il nome di fase istantanea

\frac{d Φ (t)}{d t}

è la pulsazione istantanea e misura la velocità con cui varia la fase. La frequenza istantanea è pari alla pulsazione istantanea divisa per

2 π

Siccome, in trasmissione, posso fisicamente imviare solo segnali reali, dovrò trasmettere la parte reale del segnale complesso richiamato in precedenza, quindi trasmetterò un segnale del tipo

x (t) cos (2 π f_{c} t)

Questa formula mi suggerisce l'analisi di un segnale di questo tipo:

s (t) = A (t) cos [2 π f_{c} (t) + Φ (t)]

Potrò così avere almeno due categorie di modulazioni:

Modulazioni dell'ampiezza:

quando

Φ (t) = 0

A (t) = a + b x (t)

Modulazioni d'angolo, aventi

A (t) = A_{0}

e distinte in due gruppi:

Modulazione di fase se

Φ (t) = a + b x (t)

Modulazione di frequenza se

Φ (t) = a + b \int x (t) ⅆ t

image: 1_home_maurizio_telecomunicazioni_modulazione_analogiche.jpg

2 MODULAZIONI DELL'AMPIEZZA

Se effettuo una banale moltiplicazione del segnale modulante con il segnale portante, ricordando che

cos α cos β = \frac{1}{2} [cos (α + β) + cos (α - β)]

potrò dire che:

A_{m} cos (2 π f_{m} t) \cdot A_{0} cos (2 π f_{c} t) = A_{m} A_{0} {cos [2 π t (f_{m} + f_{c})] + cos [2 π t (f_{m} - f_{c})]}

Da qui posso notare che esistono due righe spettrali laterali simmetriche rispetto alla frequenza della portante, una a frequenza

f_{c} - f_{m}

ed una a frequenza

f_{c} + f_{m}

; inoltre non ho, nello spettro, la riga relativa alla portante f

_{c}

. Se, anziché modulare con un tono puro, avessi usato una banda di frequenze, avrei ottenuto due bande di frequenze al posto delle due righe spettrali.

Quanto detto mi spinge ad alcune considerazioni distinte: in primis, l'infor-mazione è recata da entrambe le bande laterali, e ciò giustifica il nome di DSB [Double Side Band] dato a questo tipo di modulazione, la potenza trasmessa è pari al prodotto della potenza della portante per quella della modulante, l'occupazione in banda e uguale al doppio della banda della modulante ed inoltre, condizione piuttosto pesante, in ricezione devo ricostruire la portante in quanto, come visto, ne ho perso l'informazione. la prima considerazione mi spinge a sopprimere, con dei filtri, una delle due bande, ottenendo quella che è chiamata modulazione in SSB [Single Side Band]. Se sopprimo la banda laterale sinistra, avrò la USB [Upper Side Band], se, invece, sopprimo la destra, avrò la modulazione in LSB [Lower Side Band]. Mi resta sempre, però, il problema di dover recuperare la portante all'atto della demodulazione.

Posso così pensare che le condizioni necessarie per avere una modulazione d'ampiezza devono essere le seguenti:

Esiste una relazione lineare fra il valore istantaneo del segnale modulante avente frequenza angolare $f_{m}$ e l'ampiezza istantanea della radiofrequenza modulata.

Si evita che questa ampiezza scenda al di sotto dello zero, in quanto, se così fosse, si introdurrebbe una distorsione dovuta ad una variazione della fase (il cosiddetto “salto di fase” noto anche come “Phasensprung”): nell'attraversamento per lo zero la fase si inverte.

Durante le pause di modulazione si fa in modo che l'ampiezza istantanea $A (t)$ raggiunga il valore $A_{0}$ della portante non modulata.

Come conseguenza di queste tre condizioni, si vede che non basta moltiplicare

A_{0}

per

cos [2 π f_{m} t + φ]

, ma bisogna aggiungere a questo segnale una componente continua in modo che la risultante non diventi mai negativa.

Se chiamiamo

m = \frac{A_{m a x} - A_{0}}{A_{0}}

la profondità di modulazione, l'espressione generale della A(t) modulata può essere scritta come:

A (t) = A_{0} [1 + m cos (f_{m} t + φ)]

l'espressione completa del valore istantaneo risulta:

s (t) = A_{0} [1 + m cos (f_{m} t + φ)] cos (f_{c} t + Φ)

Ricordando ancora che

cos α cos β = \frac{1}{2} [cos (α + β) + cos (α - β)]

potrò scrivere che:

s (t) = A_{0} cos (f_{c} t + Φ) +

+ \frac{m A_{0}}{2} cos [(f_{c} + f_{m}) t + (φ + Φ)] +

+ \frac{m A_{0}}{2} cos [(f_{c} - f_{m}) t + (φ - Φ)]

Se analizziamo attentamente questa formula, ci accorgiamo che il segnale modulato con una sola frequenza modulante equivale alla somma di tre segnali non modulati. Questi tre segnali costituiscono le tre righe dello spettro di Fourier le cui frequenze sono così scalate:

f_{c} - f_{m}

f_{c}

f_{c} + f_{m}

. La considerazione più elementare che ci viene in mente è che ciascuna riga laterale, che si allarga fino a diventare una banda solo quando il segnale modulante non è più una sinusoide pura, dista dalla riga centrale per un valore esattamente uguale alla frequenza di modulazione, in meno per la riga inferiore, ed in più per quella superiore. Inoltre le due righe laterali hanno ampiezza uguale fra di loro e pari alla metà del prodotto

m A_{0}

, per cui risultano proporzionali alla portante, ma non superiori alla metà di essa; quest'ultimo caso, di ampiezza uguale ad

\frac{A_{0}}{2}

, si verifica con un indice di modulazione del 100 %. Se si supera tale valore si introduce una distorsione del segnale modulato, e si dice che si sta “sovramodulando”. Inoltre, continuando nell'analisi, vediamo che il segnale modulato è privo di modulazione angolare, in quanto, restando l'ampiezza istantanea sempre maggiore o uguale a 0, l'andamento della fase è descritto sempre e soltanto dal fattore

cos (Φ t + φ)

che non dipende in alcun modo dalla modulante.

Questo tipo di modulazione, prende il nome di AM [Amplitude Modulation] e si distingue dalle precedenti in quanto permette la demodulazione non coerente. La presenza delle due righe a cavallo della riga della portante giustifica il fatto che, anche in questo caso, l'occupazione in banda è pari al doppio della banda della modulante. Per questo motivo, l'AM fu il primo metodo di modulazione utilizzato.

Un quarto tipo di modulazione dell'ampiezza è la VSB [Vestigial Side Band], cioè modulazione in banda vestigiale: si conservano alcune vestigia della banda soppressa per agevolare le operazioni di ricostruzione della portante. É il metodo utilizzato per la trasmissione televisiva. In questa modulazione, che consente, rispetto alla DSB, un notevole risparmio di banda, deve essere presente la portante con una potenza pari alla metà di quella della AM ed una coda di segnale corrispondente alla banda laterale sinistra.

3 MODULAZIONI ANGOLARI

Le modulazioni angolari sono quelle in cui l'informazione viene associata alla fase del segnale portante. Un segnale modulato in fase è del tipo:

s (t) = A_{0} cos {2 π f_{c} t + ϕ [x (t)]}

in cui la dipendenza della variazione di fase

ϕ [x (t)]

dal segnale modulante x(t) è di due tipi:

$ϕ [x (t)] = k_{φ} x (t)$ , ovvero dipendenza lineare della fase dal segnale modulante, e parleremo di Modulazione di Fase o PM [Phase Modulation]

$\frac{d ϕ [x (t)]}{d t} = k_{f} x (t)$ , ovvero dipendenza lineare della derivata della variazione di fase dal segnale modulante: in questo caso è la frequenza istantanea che varia linearmente con x(t), e parleremo quindi di Modulazione di Frequenza o FM [Frequency Modulation].

Sebbene la modulazione di fase sia di importanza fondamentale nelle modulazioni digitali, è decisamente poco diffusa nelle trasmissioni analogiche, e questo perchè non solo è più difficile da realizzare, ma, soprattutto, ci consente guadagni di demodulazione molto minori rispetto a quelli raggiunti con la FM.

Un segnale s(t) modulato in frequenza da x(t) ha la forma:

s (t) = A_{0} cos [2 π f_{c} t + k_{f} \int x (t) ⅆ t]

la sua frequenza istantanea si calcola derivando la fase istantanea e dividendo per

2 π

ed è pari a

f_{i s t} = f_{c} + \frac{k_{f}}{2 π} x (t)

il termine

\frac{k_{f}}{2 π} x (t)

prende il nome di deviazione istantanea di frequenza.

Se ora consideriamo la modulante costituita da un tono puro del tipo

x (t) = cos (2 π f_{m} t)

, avremo il segnale modulato pari a:

s (t) = A_{0} cos [2 π f_{c} t + \frac{k_{f}}{2 π f_{m}} sin (2 π f_{m} t)]

Come si può vedere, il segnale modulante è periodico di periodo

\frac{1}{f_{m}}

. Se si richiede che almeno il 98% dell'energia sia compreso nelle prime N armoniche, si può dimostrare la legge di Carson, che dice che

N \overset{_{\sim}}{=} \frac{k_{f}}{2 π f_{m}} + 1

; quindi la banda al 98% del segnale modulato è definita come

B_{s} = 2 f_{m} N = 2 (\frac{k_{f}}{2 π f_{m}} + 1) f_{m}

. Il termine

\frac{k_{f}}{2 π f_{m}}

si chiama indice di modulazione. La massima deviazione di frequenza vale

f_{Δ} = \frac{k_{f}}{2 π} = \frac{k_{f}}{2 π f_{m}} \cdot f_{m}

e, quindi, la banda del segnale modulato può essere scritta nella forma

B_{s} = 2 (\frac{k_{f}}{2 π f_{m}} + 1) \cdot f_{m} = 2 (f_{Δ} + f_{m})

A seconda dei valori del termine

\frac{k_{f}}{2 π f_{m}}

si usa distinguere due tipologie della modulazione di frequenza:

Modulazione di Frequenza a Banda Stretta o NBFM [Narrow Band Frequency Modulation], per valori di $\frac{k_{f}}{2 π f_{m}} < 1$ , ed in questo caso si ha $B_{s} > 2 f_{m}$ , ossia la modulazione di frequenza non è molto differente da una modulazione d'ampiezza

Modulazione di Frequenza a Banda Larga o WBFM [Wide Band frequency Modulation], che si ha per valori di · $\frac{k_{f}}{2 π f_{m}} > 1$ . In questo caso si ha $B_{s} > 2 f_{Δ}$ ovvero la banda del segnale modulato in frequenza è praticamente indipendente dalla banda del segnale modulante.

Per le radiodiffusioni in FM si assume un indice di modulazione

\frac{k_{f}}{2 π f_{m}} = 5

, per cui, associando una frequenza della modulante massima pari a 15 kHz, la deviazione massima di frequenza sarà di 75 kHz.

4 MODULAZIONI DIGITALI

Un segnale digitale può modulare l'ampiezza, la frequenza o la fase di una portante sinusoidale. Se la forma d'onda modulante consiste in impulsi rettangolari senza ritorno a zero, allora i parametri modulati saranno spostati [in inglese Keyed] da un valore discreto all'altro. A mo' di esempio riportiamo, in figura, le forme d'onda di tre tipi di modulazione digitale, rispettivamente l'ASK [Amplitude Shift Keying] praticamente sinonimo di PAM [Pulse Amplitude Modulation], l'FSK [Frequency Shift Keying] e la PSK [Phase Shift Keying]. Per confronto, abbiamo inserito anche la forma d'onda prodotta da una modulazione di tipo DSB, dove possiamo vedere il “salto di fase” a cui si accennava in precedenza.

image: 15_home_maurizio_telecomunicazioni_modulazione_digitali.jpg

Nell'immagine:

Una rapida analisi dei tre tipi principali di modulazione, ci fa vedere come nella modulazione di ampiezza, ASK, i bit 0 o 1 sono rappresentati dalla assenza o dalla presenza della portante. Questo tipo di modulazione è anche detto di tipo on-off. La modulazione di ampiezza, è più sensibile al rumore rispetto alle altre due modulazioni digitali e richiede un banda doppia rispetto a quella occupata dal messaggio.

Per ridurre la banda occupata e la potenza di trasmissione, si ricorre a trasmissioni di tipo SSB o VSB. Per aumentare la velocità di trasmissione si sfruttano tecniche multilivello, consistenti nell'associare a multiplette di bit livelli di tensione differenti, ad esempio, associamo alla parola 00 il livello di 0 V, a 01 1 V, a 10 2 V ed a 11 3 V.

Nell'FSK, ai due livelli logici 1 e 0 corrispondono due differenti frequenze. Ad esempio, nella raccomandazione CCITT V.23 si associa allo 0 una frequenza di 2.1 kHz e all'1 quella di 1.3 kHz.

La modulazione FSK richiede una banda maggiore ispetto alla ASK, ciò a causa della presenza delle due portanti, tuttavia la si preferisce all'ASK per maggior semplicità dei circuiti di demodulazione e di rivelazione del segnale. Inoltre, essendo l'ampiezza del segnale modulato indipendente dal segnale modulante, questo tipo di modulazione sarà più insensibile ad un rumore additivo che andrà a variare proprio l'ampiezza del segnale.

Nella modulazione PSK indicata nella figura, i due valori logici 1 e 0 vanno a sfasare di 180

^{○}

il valore della fase della portante. Questo tipo di modulazione è anche chiamato BPSK [Bipolar Phase Shift Keying].

Spesso, per meglio visualizzare questi tipi di modulazione, si ricorre a rappresentazioni geometriche. La relativa raffigurazione della modulazione BPSK è riportata di seguito:

image: 3_home_maurizio_telecomunicazioni_modulazione_bpsk.png

In queste rappresentazioni la distanza dei punti dal centro rappresenta la radice quadrata dell'energia media associata al segnale.

Da questo tipo di modulazione, discende la DPSK, ovvero Differential PSK, in cui vengono trasmesse solo le differenze di fase. Ad esempio, trasmettendo un 1 logico, non cambio la fase, che verrà variata di 180

^{○}

solo in presenza di uno 0 logico.

image: 4_home_maurizio_telecomunicazioni_modulazione_dpsk.jpg

Se anziché associare la variazione di fase solo a parole di un bit, come nel caso della BPSK, associo, per ipotesi, parole di due bit, avrò sì bisogno di di

2^{2}

livelli differenti di fase, ma riuscirò a trasmettere più velocemente. Questo è il più semplice esempio di modulazione PSK multifase, la situazione per un numero

M = 4

M = 8

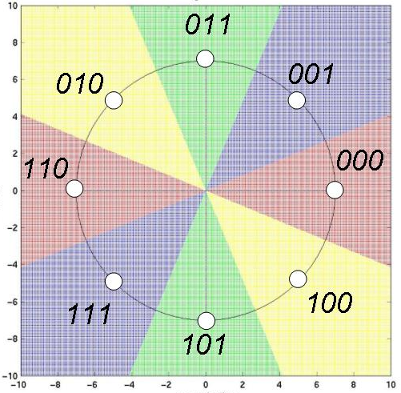
[parole di tre bit] segnali è rappresentata nelle figure seguenti:

image: 5_home_maurizio_telecomunicazioni_modulazione_4QPSK.png

image: 6_home_maurizio_telecomunicazioni_modulazione_qpsk.png

image: 7_home_maurizio_telecomunicazioni_modulazione_8psk.png

Nel caso di 4 segnali, la modulazione viene chiamata QPSK [Quaternary PSK], mentre con 8 segnali si parlerà di OPSK [Octonary PSK].

Sembrerebbe, a questo punto, facile andare a trasmettere n bit, trasmettendo

2^{n}

segnali, ognuno sfasato di

{[\frac{360}{2^{n}}]}^{o}

. Ma, supponendo di vincere le evidenti maggiori complessità circuitali, ci troveremmo esposti ad una maggiore probabilità di errore. Se, infatti, consideriamo le regioni di decisione, ovverosia le regioni in cui il mio demodulatore e, quindi, il ricevitore, decide che simbolo è stato trasmesso, vediamo che le regioni si assottigliano. Se nel caso del BPSK le due regioni di decisione erano costituite dai semipiani separati dall'asse delle ordinate, per cui, avendo, per ipotesi, trasmesso 1 ci voleva un disturbo di energia superiore a

\sqrt{ϵ}

per far sì che l'uno andasse nell'area di decisione competente allo zero e fosse quindi mal interpretato, con più punti di medesima energia è più facile che un simbolo possa essere erroneamente ricevuto. A prova di ciò basti pensare che nel caso di un QPSK con sfasamento iniziale di

4 5^{○}

, le regioni di decisione sono delimitate dagli assi coordinati, mentre in un OPSK avremo spicchi con angolo al centro pari a

{[\frac{2 π}{M}]}^{r a d}

image: 13_home_maurizio_telecomunicazioni_modulazione_regioni_colore.png

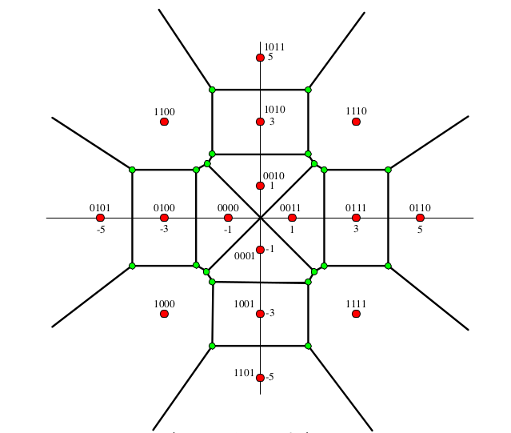
image: 16_home_maurizio_telecomunicazioni_modulazione_16qam_decision.png

Nell'immagine:

Di seguito riportiamo le simulazioni di due tipi di modulazioni (QPSK e 16 QAM) al diminuire del rapporto segnale rumore:

image: 8_home_maurizio_telecomunicazioni_modulazione_Bit_errors_30db_640.png

image: 9_home_maurizio_telecomunicazioni_modulazione_Bit_errors_15db_640.png

image: 10_home_maurizio_telecomunicazioni_modulazione_Bit_errors_10db_640.png

image: 11_home_maurizio_telecomunicazioni_modulazione_Bit_errors_6db_640.png

La prima cosa che ci viene in mente, per migliorare la probabilità di corretta ricezione, è di distanziare, fra loro, i segnali. Ciò è agevolmente fattibile aumentando l'energia associata. Così facendo, però, andiamo incontro a due serie di problemi: il primo riguarda un aumento dei costi, dell'ingombro delle strutture e, soprattutto per trasmissioni via satellite, di reperimento energetico, il secondo consiste nel fatto che, per le applicazioni tramite modem, il canale di trasmissione è costituito da cavi ed un aumento dell'energia vorrebbe dire maggior dissipazione di calore per effetto Joule e, alla lunga, comporterebbe la fusione dei cavi stessi, laddove non opportunamente dimensionati.

Per questi motivi, uniti a considerazioni relative al rapporto segnale-rumore ed all'efficienza di banda, si preferisce utilizzare una combinazione di modulazioni d'ampiezza multilivello e di fase. Per far ciò la costellazione di punti deve essere collocata sul piano in modo che aumenti il rendimento di banda senza diminuire la distanza minima fra i punti.

Il ragionamento è banale: dedicando lo stesso intervallo di tempo a trasmettere un numero doppio di segnali, la velocità di trasmissione raddoppia, quindi, a parità di energia e di prestazioni di banda, riesco a trasmettere più segnali.

Gli schemi di modulazione consistenti di due canali PAM indipendenti, ovvero quando il valore di

{log}_{2} (M)

è pari, prendono anche il nome di modulazioni QAM [Quadrature Amplitude Modulation]

Facciamo ora delle rapide considerazioni pratiche.

Nei modem servono due canali, uno per ogni direzione (ricezione e trasmissione), quindi, per la trasmissione, ad esempio, la banda utilizzabile è, al massimo, la metà della banda disponibile. Se, poi, usiamo l'FSK avremo bisogno di due portanti per due forme d'onda ortogonali, il che vuol dire che usa uno spazio di dimensione 2 per trasmettere un bit. Nel BPSK il numero di bit per dimensione è 1, nel 4-PSK è di

2 : 2 = 1

. Nel 16-QAM si hanno 4 bit per 2 dimensioni, ovvero 2 bit per dimensione. Quanto più cresce il numero di bit per dimensione, tanto più possiamo andare veloci.

Storicamente, negli anni `20, Nyquist considerava il prodotto

2 W T = 1

, essendo W la larghezza di banda e T il periodo, e costruiva segnali monodimensionali.

Negli anni `50, grazie alla teoria dell'informazione di Shannon, possiamo teoricamente trasmettere M segnali in n dimensioni. La quantità di informazione per bit è

\frac{{log}_{2} M}{n}

, essendo il tempo T, la velocità di trasmissione sarà

R = \frac{{log}_{2} M}{T}

. Ciò vuol dire che, se aumento il numero di dimensioni, riuscirò a trasmettere più informazione alla stessa velocità, ovvero posso aumentare, a parità di banda, la velocità di trasmissione. In altri termini, la banda non limita la velocità di trasmissione.

Nel caso di 2 bit a dimensione, il limite sulla banda è di 16 kbit/sec. con un rapporto di 4 ottengo 32 kbit/sec.

Per poter costruire modem veloci, è stato considerato lo spazio dei segnali bidimensionali (4-PSK o 16-QAM). Shannon aveva già osservato che ci può essere, nelle trasmissioni, un guadagno dovuto all'incremento della dimensione nello spazio dei segnali e la velocità dipende non più da T e da W, ma da M; T e W sono interscambiabili. Quindi posso ignorare la limitazione dovuta alla ristretta banda telefonica o alla limitazione sul canale e posso, quindi, trasmettere ad alta velocità su di una banda limitata.

Ricordando, però, che la potenza è data dal prodotto del numero di bit al secondo per l'energia per bit, e che, comunque, a bassa energia associata corrisponde una maggiore probabilità di errore, il limite fisico è costituito proprio dalle dimensioni dei cavi, anche se è dimostrabile che aumentando la dimensione degli spazi, si migliora anche in termini di probabilità di errore. É stata realizzata una configurazione con

M = 16

n = 4

R = 1

. Quindi si trasmette 1 bit per dimensione. La forma geometrica della costellazione è una sfera. in questo caso il prodotto

2 W T = 2

Le considerazioni sembrano intuitive se guardiamo la figura seguente, caso semplicissimo di una struttura a tre segnali:

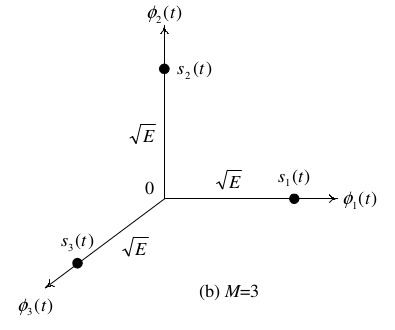
image: 17_home_maurizio_telecomunicazioni_modulazione_3d.png

Sebbene queste tecniche di modulazione siano tecniche a larga banda, in quanto si paga un po' di più in termini di occupazione di banda, in realtà i vantaggi sul migliore utilizzo della potenza derivante da una netta diminuzione dell'errore, che conseguono dall'utilizzo di prodotti 2WT crescenti, giustificano gli sforzi tecnologici che, al momento, si stanno compiendo. Giusti compromessi fra potenza ed errore sono raggiunti non solo con l'ottimizzazione dei ricevitori e con la scelta oculata di particolari forme d'onda, ma anche grazie all'uso di codifiche a controllo d'errore. Codici come quello di Reed & Solomon, utilizzato nella realizzazione dei CD audio (che può essere tranquillamente visto come canale trasmissivo), permettono di forare, letteralmente, il supporto con un foro da 1 cm di diametro senza che si noti, all'ascolto, alcun tipo di errore: l'informazione è perfettamente giunta a destinazione.

Un brevetto del 2012, consultabile alla URL

http://www.faqs.org/patents/app/20120140614

dal titolo “OFDM APPARATUS USING THREE-DIMENSIONAL HEXADECIMAL SIGNAL CONSTELLATION” ci dà un'idea degli sforzi in tal senso:

image: 18_home_maurizio_telecomunicazioni_modulazione_20120140614_11.png

CENNI ALLA MODULAZIONE

1 GENERALITA'

2 MODULAZIONI DELL'AMPIEZZA

3 MODULAZIONI ANGOLARI

4 MODULAZIONI DIGITALI