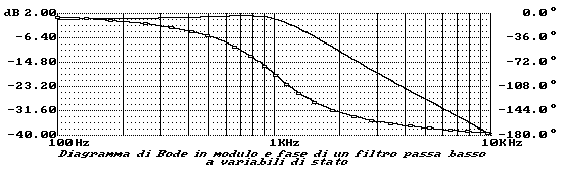Torna alla Home Page
Maurizio Monteduro
Prima di addentrarci nell'analisi dettagliata dei filtri attivi, giova tentare di dare una definizione al termine filtro.
Un filtro è un doppio bipolo che, una volta inserito fra generatore ed utilizzatore, fornisce a quest'ultimo la massima potenza quando la frequenza del segnale applicato all'entrata è compresa fra uno o più intervalli di frequenze, ciascuno dei quali prende il nome di banda passante, mentre impedisce la trasmissione del segnale nel campo, o nei campi, di frequenze complementari ai precedenti, ciascuno dei quali prende il nome di banda attenuata.
In relazione al comportamento in frequenza presentato dei filtri stessi, è possibile effettuare una prima distinzione: i tipi più diffusi sono i seguenti:
Il filtro Passa Basso presenta la banda passante per frequenze da 0 a f0, mentre la banda attenuata va da f0 all'infinito.
Il filtro Passa Banda ha la banda attenuata da 0 a f1, passante da f1 a f2 ed ancora attenuata da f2 all'infinito.
Il filtro Passa Alto palesa la banda attenuata da 0 a f0 e passante da f0 all'infinito.
Il filtro a Reiezione di Banda o "filtro elimina banda" è il complementare del filtro passa banda, pertanto presenterà la banda passante da 0 a f1, attenuata da f1 a f2, ed ancora passante da f2 all'infinito.
Il filtro Passa Tutto ha la proprietà di non variare il modulo della sua funzione di trasferimento al variare della frequenza, ma presenta una rotazione di fase di 360° attorno ad una data frequenza.
Senza addentrarci minimamente nella complessa teoria che sta alla base della sintesi dei filtri passivi, ci basti pensare che, normalmente, un filtro passivo presenta un numero di induttori circa pari al numero di condensatori che lo compongono. Gli induttori sono i componenti che danno la maggior quantità di problemi sia nella loro costruzione che nel loro utilizzo, infatti sono generalmente ingombranti, costosi, scarsamente integrabili e presentano una buona dose di parametri parassiti che allontanano il funzionamento pratico da quanto ci si attenda dal calcolo teorico del filtro. Si è quindi cercato di orientarsi su celle che utilizzino solo resistori e condensatori, tentando di ovviare all'assenza di induttori con l'uso di componenti attivi, prevalentemente amplificatori operazionali. Simili circuiti vengono generalmente definiti Circuiti RC Attivi.
In questo capitolo affronteremo inizialmente il problema della
simulazione di induttori, per poi addentrarci nello studio di
diverse soluzioni circuitali per la realizzazione dei vari tipi
di filtro.
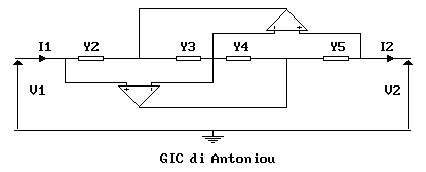
Per il circuito in figura, vogliamo calcolare i parametri di catena
A,B,C,D: tali parametri sono i coefficienti delle incognite del
sistema:
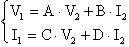
Per valutare AºV1/V2
con I2=0 basta osservare che, nell'ipotesi di operazionali
ideali, non essendoci caduta di tensione fra i morsetti invertente
e non invertente, l'ingresso è equipotenziale all'uscita,
pertanto V1=V2 e quindi A=1. Per il calcolo
relativo a BºV1/I2
con V2=0, per lo stesso motivo precedente, anche V1
sarà nullo, e pertanto B=0. Per quanto concernente CºI1/V2
con I2=0, ovvero con l'uscita a vuoto, basta notare
che, essendo l'operazionale ideale ed essendo nulla la corrente
I2, sarà nulla anche la corrente che circola
in Y5. Ciò vuol dire che sarà nulla la
caduta di tensione ai capi di Y5 e non essendoci differenza
di potenziale fra i morsetti invertente e non invertente dell'operazionale,
non ci sarà caduta di tensione nemmeno su Y4,
il che si traduce nell'asserzione che anche la corrente che circola
in Y4 dovrà essere nulla. Non entrando corrente
negli operazionali ed essendo nulla la corrente in Y4,
dovrà essere nulla anche la corrente che circola in Y3
e quindi, su di essa, non ci sarà caduta di tensione. Tenendo
presente che essendoci un potenziale nullo fra i due morsetti
dell'operazionale, sarà nulla la caduta su Y2
e quindi sarà nulla anche la corrente che vi circola. Non
entrando corrente nel morsetto non invertente dell'operazionale,
se ne deduce che anche I1 sarà nulla, e quindi
C=0.
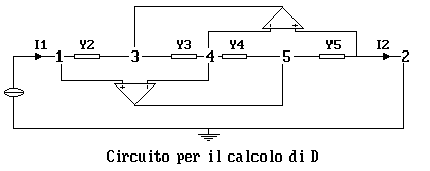
Calcoliamo ora DºI1/I2
valutato con V2=0, ovvero con l'uscita chiusa in corto
circuito, così come da figura. Essendo l'uscita chiusa
in corto circuito, la tensione ai nodi 1, 2 e 4 sarà nulla,
in quanto V2 è nulla a causa del corto circuito,
V4 è nulla in quanto ai morsetti di ingresso
di un operazionale non cade tensione, e V1 è
pari a 0 V per lo stesso motivo. A questo punto non resta che
risolvere le equazioni ai nodi 3 e 5, ricordando, come sempre,
che essendo gli operazionali ideali, non entra corrente nei loro
morsetti di ingresso.
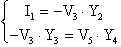[equazioni rispettivamente ai
nodi 3 e 5]
Inoltre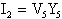 
Risolvendo il sistema, otteniamo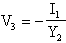 
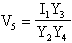
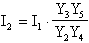
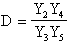
e 
da cui, sostituendo, 
e quindi 
.
Quindi il sistema risulta essere:
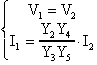
Se ora carichiamo l'uscita con un'impedenza ZL, osservando
che vale la relazione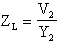 
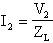
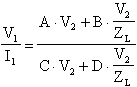
ovvero 
,
calcoliamoci l'impedenza di ingresso Zing che si vede
guardando fra il morsetto 1 e la massa; essa sarà pari
a 
, cioè:
Semplificando V2 e facendo il m.c.m. potremo scrivere che:
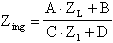
Sostituendo i nostri parametri di catena, potremo scrivere che nel caso in analisi, l'impedenza di ingresso Zing vale:
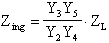
Resta evidente, a questo punto, che se al posto di Y3 mettessimo un condensatore di capacità C3 e al posto delle restanti ammettenze Yi mettessimo altrettante resistenze di valore Ri, la Zing diventerebbe:
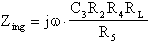
che ha le dimensioni, come si può ben notare, di un'impedenza con un capo a massa. Lo stesso ragionamento vale se sostituissimo Y5 con una capacità di valore C5 e, come prima, tutte le altre ammettenze con delle resistenze. In questo caso otterremmo:
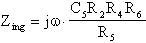
I circuiti relativi sono riportati in figura.
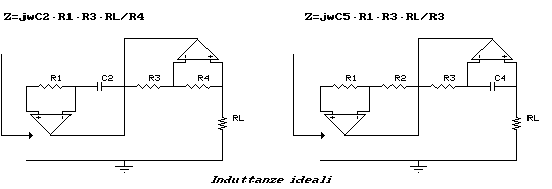
Con questo tipo di circuito, siamo quindi in grado di simulare induttanze ideali con un capo a massa. É facile dimostrare, e lo lasciamo all'attento lettore, che per realizzare induttanze fluttuanti, cioè sospese, ovvero senza capi a massa, sarà necessaria la connessione di due induttanze ideali come indicato nella figura che segue.
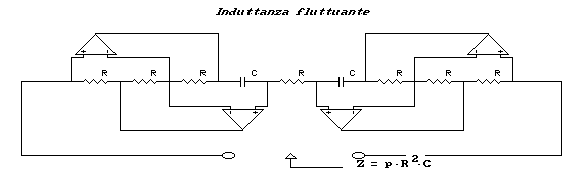
É possibile, con giuste sostituzioni, realizzare, a questo
punto, circuiti che abbiano impedenza di ingresso proporzionale
a p². Ricordando che p º
jw e che quindi p² = -w²,
potremo avere dispositivi con impedenza puramente reale e proporzionale
a -w². Se l'impedenza è
puramente reale, allora presenterà un comportamento resistivo
negativo. Questi circuiti sono stati, da Bruton, denominati "FDNR",
acronimo di Frequency Dependent Negative Resistance, ovvero di
resistenze negative dipendenti dalla frequenza. Si ottengono così
FDNR detti di tipo D o di tipo E a seconda che siano proporzionali
rispettivamente a 1/p² o a p². Nel primo caso otterremo
dei "Supercondensatori", mentre nel secondo caso avremo
dei "Superinduttori". É banale, sostituendo nell'equazione
già calcolata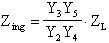 
al posto delle ammettenze
indicizzate le reali ammettenze dei componenti circuitali, dimostrare
che, nei supercondensatori, Y(p) sarà proporzionale a p²
e, nei super induttori, sarà Z(p) ad essere proporzionale
a p². La costante di proporzionalità sarà un
numero sempre positivo che prende il nome di "D" nel
caso dei supercondensatori e di "E" nell'altro caso.
D ha le dimensioni di Farad per Secondo, mentre E si misura in
Henry per Secondo, come per altro, è facile dimostrare.
I circuiti che si ottengono sono rappresentati nelle figure seguenti:
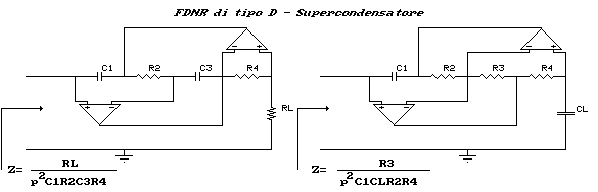
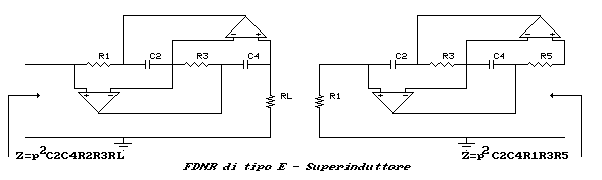
Entriamo ora nell'analisi più dettagliata dei filtri attivi.
In questo capitolo, ci soffermeremo soprattutto sui filtri del
secondo ordine, ovvero su filtri che hanno a denominatore un polinomio
di secondo grado nella forma: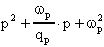 
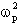
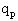
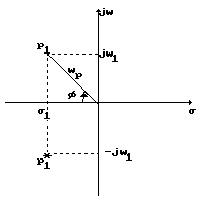
, in cui
è il modulo dei poli complessi,
mentre 
è il fattore di qualità
del filtro, pari all'inverso del fattore di smorzamento
d Vale la pena di puntualizzare
brevemente il significato fisico di w
e di q. Risolvendo l'equazione sopra riportata, risulterà
evidente la comparsa di una coppia di poli, non necessariamente
puramente reali, ma complessi coniugati. La distribuzione dei
poli sul piano gaussiano sarà quindi, genericamente, quella
riportata in figura:
Sia quindi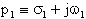 
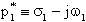
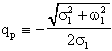e 
con s1 reale e w1
reale e positivo. A questo punto, qp e wp
sono così definiti:
e
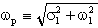
da cui è facile dedurre che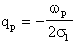 
É evidente osservare che wp
è il modulo dei poli complessi, mentre qp risulta
essere pari a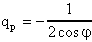 
. Si può, così,
notare come il q cresca da 0.5, quando le radici sono reali, fino
a tendere a ¥ se le radici sono
puramente immaginarie.
Il polinomio di secondo grado che genera una simile coppia di poli sarà:
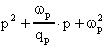
ed il generico polinomio non monico di secondo grado
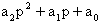
avrà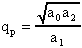 
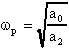
ed 
Volendo chiamare s1 e s2
le radici reali negative del trinomio monico, lo stesso acquisterà
la forma di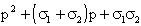
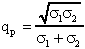
. In questo caso
ed 
Come abbiamo avuto modo di vedere all'inizio del capitolo, esistono
cinque classi fondamentali di filtro. A queste classi corrispondono
almeno altrettante funzioni di trasferimento in tensione dei filtri
stessi. In questa rapida trattazione ci occuperemo solo di funzioni
di secondo grado, che conducono ad avere filtri con due poli e
con un numero di zeri massimo pari, evidentemente, a due. La funzione
più generale in grado di dar luogo, come vedremo, a tutte
le celle elementari di filtro, è la funzione biquadratica
che ha espressione del tipo:
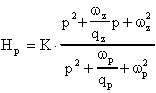
Il modulo di questa funzione, ricordando che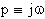
,
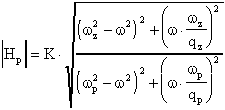
sarà:
ed il suo argomento
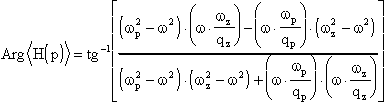
É particolarmente semplice pensare come, al variare del
numeratore, sia possibile realizzare tutti i tipi elementari di
filtro di secondo ordine. Infatti un Filtro Passa Basso (Low
Pass Filter) del secondo ordine, avrà funzione
di trasferimento pari a :
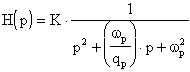
tracciando i diagrammi del suo modulo e della sua fase risulta
chiara la denominazione di questa funzione, che nel prosieguo
verrà indicata come LP, infatti:
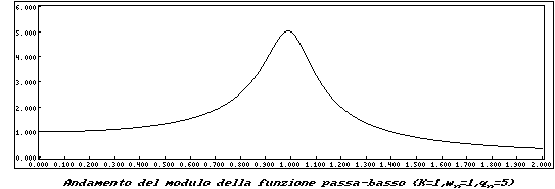
e lo studio della sua fase produrrà il seguente grafico:
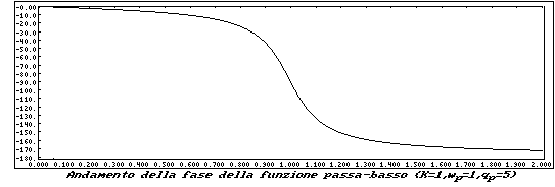
La funzione Passa Banda dovrà presentare uno zero
nell'origine. Sarà quindi del tipo:
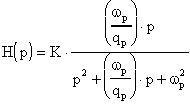
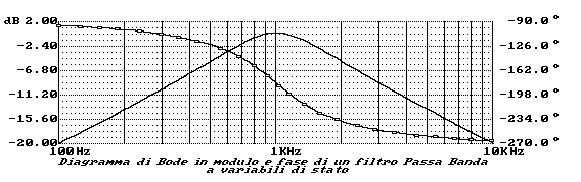
Anche per questa funzione tracciamo i grafici relativi al suo
modulo ed alla sua fase:
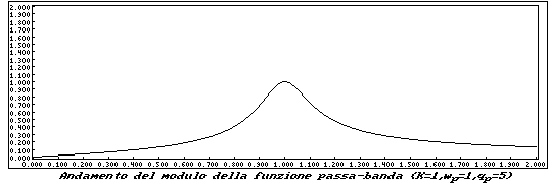
É facile riconoscere un massimo che cade per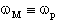 
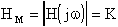
il cui valore, in ordinata, risulta pari a 
Definendo w1 ed w2
le frequenze di taglio, per le quali il modulo si riduce di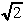 
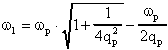
(3dB), è possibile costruirsi un importante risultato per
qp. Infatti:
ed
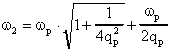
ricavando qp da queste due si ottiene:
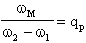
Da questa relazione si evince che il Q dei poli risulta essere il rapporto fra la pulsazione (frequenza) di risonanza wM, che, per altro, è coincidente con wp e la banda passante del filtro.
Tracciamo ora il diagramma della fase della funzione passa banda:
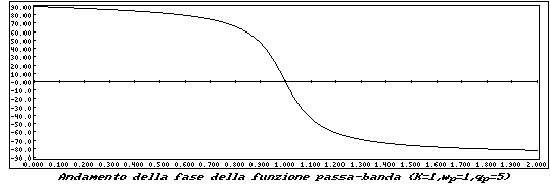
L'ultima funzione di questo tipo che dobbiamo considerare è
la funzione Passa Alto, di seguito indicata con HP.
Essa presenterà due zeri nell'origine e sarà, pertanto:
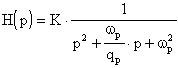
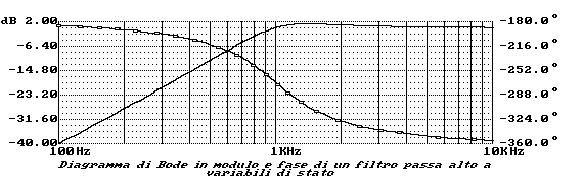
Tracciamone i soliti grafici.
Il Diagramma del modulo sarà:
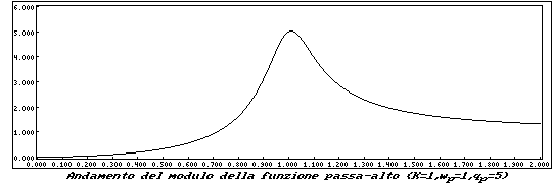
e quello della fase risulterà essere:
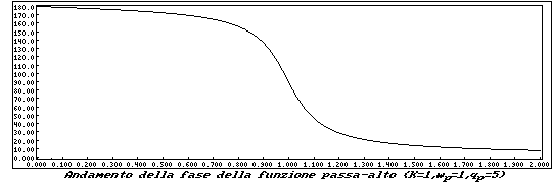
Un'altra importante categoria di filtri sono quelli aventi funzione di trasferimento con zeri di trasmissione finiti, o filtri di notch. In inglese il termine "notch" ha il significato di "incavo a V" e pertanto, generalmente, si associa la definizione di "filtri di notch" solo ai filtri a reiezione di banda. In realtà, una definizione più rigorosa attribuisce il termine "notch" anche alle funzioni passa basso e passa alto aventi le caratteristiche che andremo ad illustrare.
La generica funzione con zeri di trasmissione finiti è
del tipo:
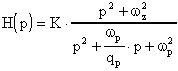
Chiaramente, potremo avere tre distinti casi:
1) 
:
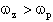
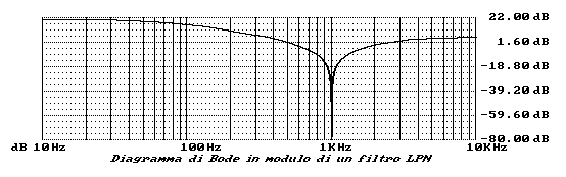
É il caso di una funzione di tipo Passa Basso con una coppia di zeri di trasmissione immaginari. Prende il nome di Lowpass notch (LPN)
2) 
:
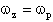
In questo caso ho un minimo pari a 0 in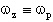 
ed è pertanto una funzione elimina banda o a Reiezione
di Banda (Band Rejection) (BR)
3) 
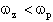
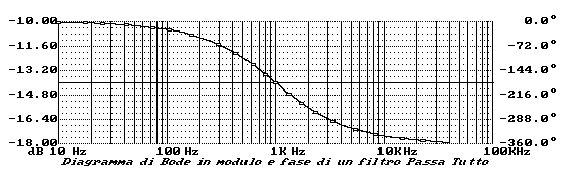
La funzione è ora di tipo Passa Alto con zeri di trasmissione puramente immaginari. Prende il nome di Highpass Notch (HPN)
I grafici relativi sono di seguito riportati.
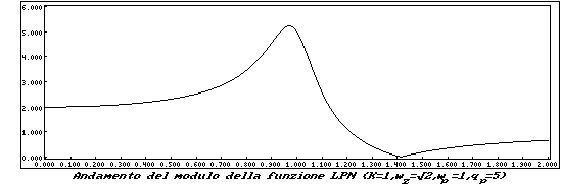
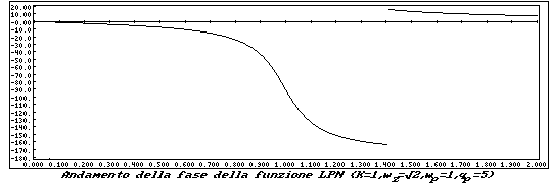
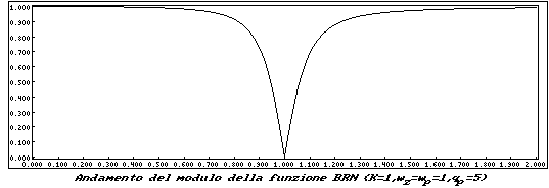
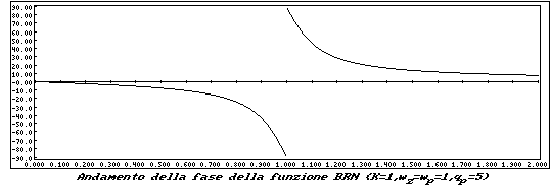
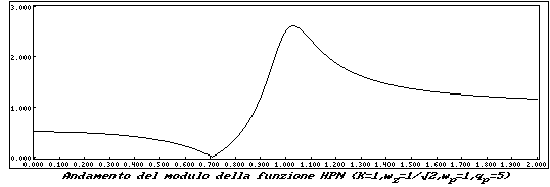
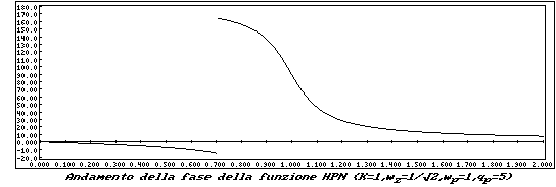
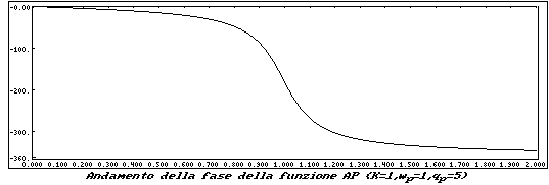
L'ultima funzione che prenderemo in esame, è la funzione Passa Tutto, o All Pass (AP).
Presenta una funzione del tipo:
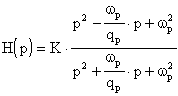
Il suo modulo è costante al variare della frequenza e vale
K, mentre la fase passa da 0° in continua a -360° per
frequenza infinite. Lo sfasamento di -180° cade in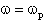 
.
É quindi un tipico filtro sfasatore.
I diagrammi relativi sono riportati nelle seguenti illustrazioni:
Potrebbe essere un buon esercizio, e lo si lascia al lettore, il computo del modulo e della fase delle varie funzioni, come dei loro massimi e minimi. Come suggerimento, si consiglia di dividere il parte pari e parte dispari il numeratore ed il denominatore della funzione di trasferimento, seguendo quanto di seguito indicato.
sia:
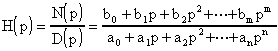
e siano:
Risulta:
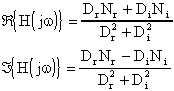
É facile, a questo punto, ricavare il modulo e la fase (argomento o anomalia, come più correttamente indicano i matematici)
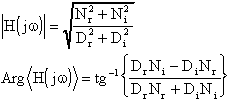
Abbiamo così terminato l'esame delle principali funzioni
di secondo ordine. Non resta, ora, che vedere come possano essere
realizzate circuitalmente.
Supponiamo di voler realizzare un filtro attivo del secondo ordine
di qualsiasi tipo. Sceglieremo un amplificatore operazionale come
elemento attivo, dato che, presentando guadagno pressochè
infinito, la funzione di trasferimento del circuito dipende praticamente
solo dalla reazione, e ci orienteremo su un circuito del tipo
di quello riportato in figura, considerando che è il circuito
più semplice che ci possa venire in mente.
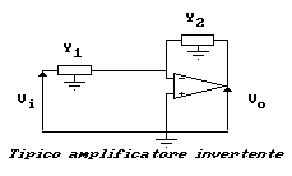
É banale calcolare la funzione di trasferimento del circuito, ricordando che con Y vengono indicate le ammettenze (inverso delle impedenze). Essa sarà semplicemente:
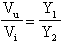
in cui Y1 ed Y2 sono le ammettenze di generici doppi bipoli RC comunque costituiti.
Procedendo alla sintesi del filtro, ci accorgeremmo che non solo saremmo chiamati a risolvere calcoli talvolta piuttosto complessi, ma giungeremmo alla realizzazione di reti comprendenti un numero spesso ridondante di componenti.
Si preferisce, così, ricorrere a strutture a reazioni multiple,
come quella di seguito indicata:
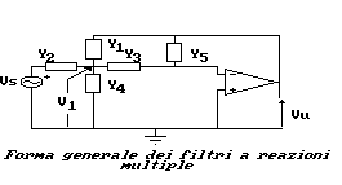
Calcoliamo la funzione di trasferimento di questo circuito.
Nel seguito denomineremo Ii la corrente che circola
nella generica ammettenza Yi. Ricordando che l'amplificatore
operazionale è, in questo primo caso, considerato ideale
e che, pertanto, ai suoi morsetti di ingresso non vi è
caduta di tensione, considerando quindi il morsetto invertente
come massa virtuale, potremo dire che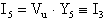 
;
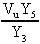
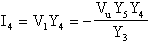
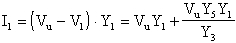
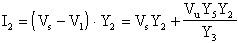
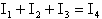
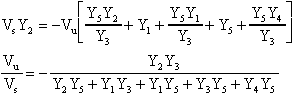
questa corrente, non potendo entrare nell'operazionale, genera
una caduta di tensione su Y3 pari a 
.
Questa tensione è uguale ed opposta a quella che cade su
Y4. La corrente uscente dal nodo nel quale confluiscono
Y1, Y2, Y3 ed Y4 e
circolante in Y4 sarà quindi 
,
avendo definito con V1 la tensione fra quel
nodo e massa. La corrente I1 sarà pari a 
ed 
. Dobbiamo a questo punto risolvere
l'equazione al nodo
. Pertanto:
ovvero
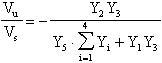
Se l'amplificatore operazionale, anzichè presentare guadagno
infinito (essere, cioè, ideale) presentasse guadagno µ,
il potenziale del morsetto invertente non sarebbe più a
potenziale di massa, ma si troverebbe ad una tensione pari a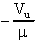 
pertanto le equazioni diventerebbero:
mettendo a sistema le equazioni I, III, IV, V, VI e svolgendo
i calcoli si giunge alla funzione di trsferimento:
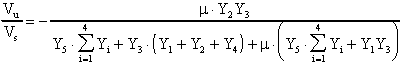
A questo punto, conoscendo i vari tipi di funzione del secondo
ordine e la funzione di trasferimento generale della rete a reazioni
multiple, è possibile, sostituendo alle ammettenze Yi
o resistenze o capacità, ottenere qualsiasi di filtro,
in questo caso, invertente. Vediamo i vari casi:
La funzione passa basso non presenta zeri, pertanto Y2 ed Y3 saranno resistenze.
Dovendo a questo punto realizzare una coppia di poli, non potremo fare altro che porre Y5 ed Y4 capacità ed Y1 resistenza. Infatti se Y1 fosse una capacità e le altre resistenze, otterrei una funzione di primo ordine, dovrei necessariamente avere anche Y5 come capacità per ottenere il termine di secondo grado, ma, così facendo, perderei il termine noto. Quindi la scelta è obbligata. Inoltre, basti pensare che, in un filtro passa basso, la continua deve poter passare, pertanto siamo strettamente vincolati sullo scegliere Y2 ed Y3 come resistenze, in quanto se almeno una fosse un condensatore, questo si comporterebbe come condensatore di blocco.
Il circuito che si ottiene è il seguente:
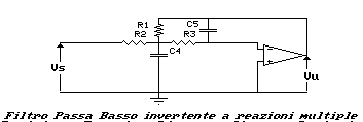
La funzione di trasferimento di questo filtro può essere
ottenuta o per via diretta dal circuito o, più semplicemente,
sostituendo al posto delle Yi i valori delle ammettenze
proprie, quindi avremo:
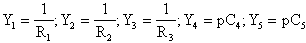
Si otterrà:
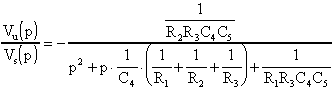
Il guadagno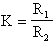 
La pulsazione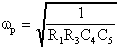 
Il termine 
Si lascia la verifica al Lettore.
Il filtro Passa Banda presenta diverse soluzioni circuitali. Fra
tutte se ne analizza una delle più pratiche:
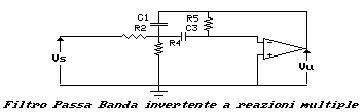
La funzione di trasferimento sarà:
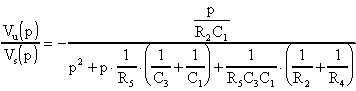
Il guadagno 
La pulsazione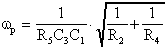 
Il termine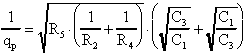
É sottinteso che gli stessi ragionamenti fatti per ricavare
il filtro Passa Basso, sono validi anche per il Passa Banda e
per il prossimo filtro che vedremo: il Passa Alto.
Il filtro Passa Alto a reazioni multiple invertente viene realizzato
seguendo lo schema appresso riportato:
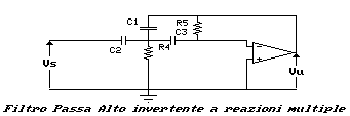
Anche per questo filtro si danno le relazioni caratteristiche:
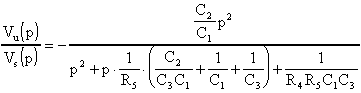
Il guadagno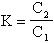 
La pulsazione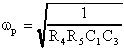 
|
Il termine 
Quella presentata è solo la più generale rassegna di filtri invertenti a reazioni multiple. Altri filtri del secondo ordine potranno essere progettati seguendo i normali dettami della teoria delle reti elettriche.
Per fare un bilancio delle configurazioni sin qui viste, dobbiamo
notare che un grande vantaggio di questo tipo di filtri, è
quello di presentare impedenza di uscita decisamente bassa, ciò
vuol dire che questi filtri possono essere posti come stadi piloti
di altri circuiti, ottenendo così un fattore di inserzione
trascurabile. Un grosso svantaggio, invece, è rappresentato
dal fatto che non è possibile ottenere alti valori di Q,
e quindi alte selettività, senza dover ricorrere ad elementi
passivi di valore compreso all'interno di un grande campo. La
realizzazione di filtri a reazioni multiple con circuiti a reazione
positiva, può superare tali limitazioni.
Consideriamo, preliminarmente, il ben noto amplificatore di tensione
non invertente:
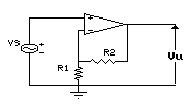
La sua funzione di trasferimento è:
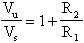
Questo circuito può essere considerato come un insieme
unico di amplificatore reazionato, in cui la rete ß di reazione
è costituita dal partitore fra R1 ed R2.
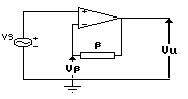
Se chiamiamo Vb la tensione
ai capi di R1, il fattore di reazione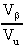 
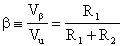
sarà dato da:
Chiamando ora m il guadagno dell'amplificatore
retroazionato ed A l'amplificazione dell'amplificatore
operazionale, potremo dire che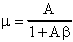 
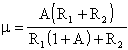
e quindi
Nel caso in cui A = ¥ la formula
si riduce a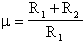 
uguale, per altro, a quella
già vista.
Consideriamo una struttura del come quella rappresentata in figura.
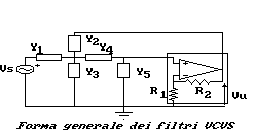
Calcoliamo, anche in questo caso, la sua funzione di trasfermento,
tenendo conto di quanto detto in precedenza, ovvero che, supponendo
l'operazionale ideale, sarà possibile dire che il guadagno
della parte racchiusa nel riquadro sia pari a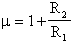 
.
Pertanto si terrà conto di ciò nei nostri calcoli,
tenendo presente che la tensione di uscita sarà pari a
m volte la tensione presente
sel morsetto non invertente dell'operazionale.
Procedendo come di consueto, calcoliamoci la funzione di trasferimento
.
; la tensione ai capi di Y3,
chiamata V3 sarà:
; quindi 
.
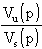
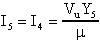
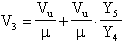
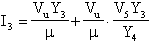
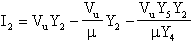
ed infine
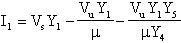
scrivendo l'equazione al nodo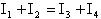 
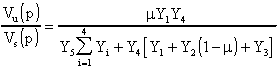
e sostituendo,
otteniamo:
In questo paragrafo, ricaveremo lo schema dei vari filtri (LP, BP, HP) che realizzano le relative funzioni. Sono possibili più soluzioni circuitali che implementino i diversi tipi di filtri, come, per altro, il Lettore potrà facilmente verificare, sia invertenti che non invertenti, ma noi analizzeremo solo le configurazioni proposte da Sallen e Key. Per inciso, questi circuiti prendono normalmente il nome di VCVS, acronimo di Voltage Controlled Voltage Source (Sorgente di Tensione Controllata in Tensione).
Iniziamo così col vedere il filtro Passa Basso; va da sè che il ragionamento che conduce alla realizzazione dei filtri è lo stesso visto per i circuiti a reazioni multiple.
Il filtro Passa Basso non invertente VCVS di Sallen & Key
è realizzato secondo il seguente schema circuitale:
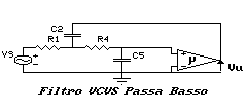
La funzione di trasmissione di questo filtro sarà:
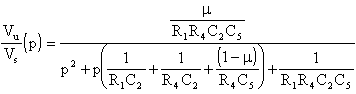
Il guadagno K = µ
La pulsazione 
ed il fattore 
La configurazione di Sallen & Key del filtro Passa Banda VCVS
non invertente è la seguente:
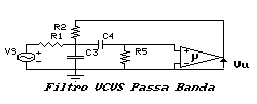
La funzione di trasmissione di questo filtro sarà:
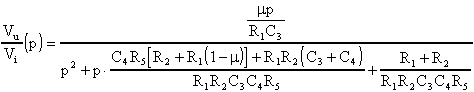
Il guadagno
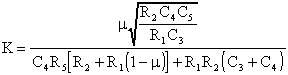
La pulsazione 
ed il fattore 
Il filtro Passa Alto di Sallen & Key non invertente è:
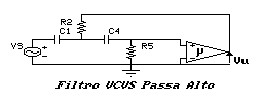
Anche di questo filtro si forniscono i parametri di rete caratteristici:
La funzione di trasmissione è:
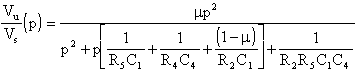
Il guadagno K = µ
La pulsazione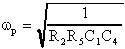 
|
ed il fattore 
Terminata questa breve rassegna di filtri VCVS è doveroso
porre alcune considerazioni di carattere generale al loro riguardo.
Innanzitutto dobbiamo notare come il fattore qp, sebbene
possa essere regolato agendo su µ in modo indipendente da
wp, sarà sempre funzione
di K. Inoltre wp può
essere regolato indipendentemente da qp solo per i
filtri passa alto e passa basso, ma non per il passa banda. In
ultimo si nota che le caratteristiche generali dei vari filtri
saranno comunque sensibili alle variazioni del guadagno µ.
Continuando nella nostra piccola rassegna di filtri, meritano un importante cenno i cosiddetti Filtri a Variabile di Stato. Questi filtri, che alcune case come la BURR-BROWNâ, ropongono come filtri universali integrati, hanno il pregio di palesare un qp meno sensibile alle variazioni degli elementi costitutivi il circuito rispetto alle configurazioni già viste, e quindi simili circuiti, che presentano lo svantaggio di necessitare di un maggior numero di componenti, vengono di preferenza utilizzati per realizzare dispositivi con qp > 50.
Supponiamo di voler realizzare la seguente funzione di trasferimento
biquadratica:
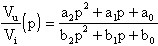
dividiamo numeratore e denominatore per p² ottenendo:
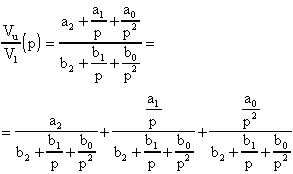
É facile notare come il primo membro descriva una funzione di tipo Passa Alto, il secondo una Passa Banda ed il terzo una Passa Basso.
Possiamo, a questo punto, incominciare a realizzare questa funzione
di trasferimento:
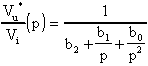
Elaborando questa formula, possiamo scrivere che:
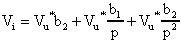
e quindi
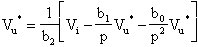
Riprendiamo per un istante il noto circuito integratore senza
perdite, o ideale, e calcoliamoci la sua funzione di trasferimento
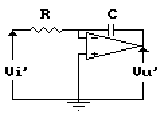
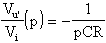
che è una funzione di trasferimento ad un sol polo, col polo nell'origine.
É abbastanza obbligato pensare che potrò realizzare
tutti i poli della mia funzione di trasmissione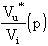 
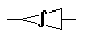
con degli integratori di questo tipo, che indicherò col
simbolo seguente:.
Otterrò, così facendo, un circuito del tipo:
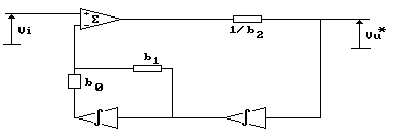
Banalmente, ora, potrò ricostruire tutta la funzione di
trasferimento completa, moltiplicando le tre uscite dai tre blocchi
bi per i rispettivi coefficienti ai e sommando i tre
segnali, ottendo un circuito il cui schema a blocchi è
il seguente:
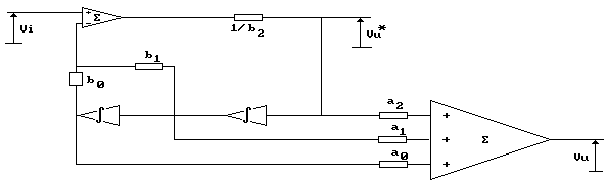
Prelevando l'uscita dopo il blocco a0 otterrò la funzione
passa basso:
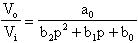
prelevando, invece, il segnale dopo il blocco a1 otterrò
la funzione passa banda:
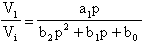
prelevando, infine, il segnale dopo il blocco a2 otterrò
la funzione passa alto:
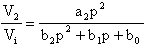
Possiamo, a questo punto, facilmente ricavarci lo schema elettrico del circuito che realizza la funzione cercata, sostituendo banalmente agli integratori il loro schema precedentemente ricordato, rammentandoci che l'integratore è invertente e quindi che l'uscita del primo integratore andrà sottratta dall'ingresso, ed eliminando il sommatore finale che non avrà più senso per realizzare i tre filtri base.
La BURR-BROWNâ, nel suo filtro universale attivo UAF41, integra, però, anche un quarto amplificatore operazionale che lascia sconnesso; esso serve o per essere usato come amplificatore invertente, o, come vedremo nella prossima sezione, per realizzare un filtro a reiezione di banda.
Lo schema elettrico del circuito completo verrà ad essere
il seguente:
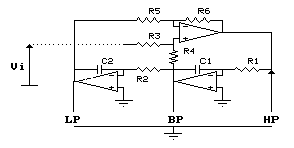
In figura sono state indicate le uscite LP (Passa Basso), BP (Passa Banda) e HP (Passa Alto).
Per esercizio, calcoliamoci la funzione di trasferimento delle
tre uscite considerate, ricordando che il segnale che esce da
ogni integratore sarà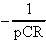 
volte quello
che entra.
Chiamando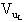 
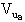
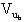
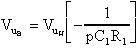
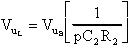
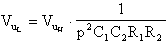
l'uscita del passa basso, 
l'uscita del passa banda e 
l'uscita del
passa alto, potremo inizialmente dire che 
e che 
e quindi 
Chiamando V- la tensione al morsetto invertente dell'operazionale
usato come sommatore, avremo:
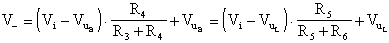
sostituendo i valori prima calcolati per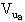 
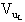
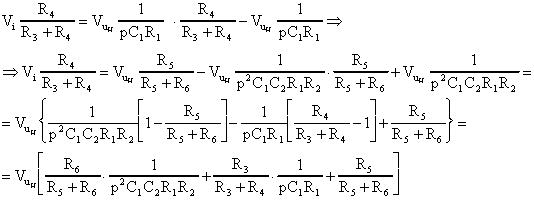
e 
e svolgendo i calcoli, scriveremo:
quindi: 
ordinando i termini e ponendo la funzione in forma monica si ottiene:
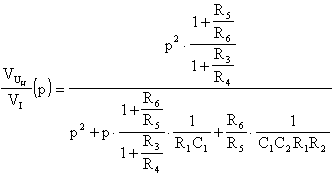
Ricordando che
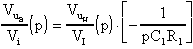
sarà facile dire che
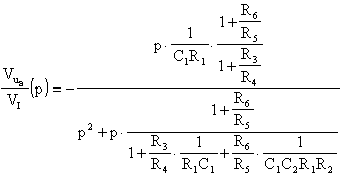
Parimenti, ricordando che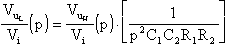 
sarà agevole scrivere la funzione di trasmissione del filtro Passa Basso:
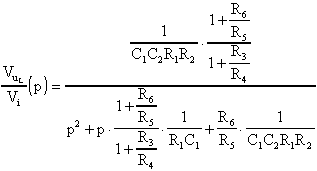
Da quanto detto, possiamo notare innanzitutto che il filtro Passa Banda è invertente, quindi, se ciò può disturbare, bisognerà fare seguire l'uscita da un amplificatore invertente che mi rimetta l'uscita in fase con l'ingresso, inoltre, tutti questi filtri possono essere sintonizzati variando simultaneamente o R1 ed R2 o C1 e C2, mentre il Q può essere regolato indipendentemente agendo su R4. In ogni caso, però, il guadagno K non sarà mai indipendente. Infatti, avendo tutti i filtri, lo stesso denominatore nella funzione di trasferimento, i parametri caratteristici saranno:
la pulsazione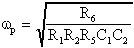 
|
il fattore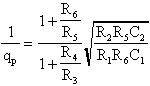 
uguali per tutti i filtri, mentre i guadagni K, diversi da configurazione
a configurazione, saranno quelli di seguito riportati:
Filtro Passa Basso:
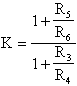
Filtro Passa Banda:
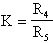
Filtro Passa Alto:
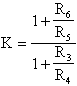
Come abbiamo potuto osservare nel paragrafo precedente, alcune case costruttrici producono e commercializzano dispositivi integrati che siano in grado di realizzare i tre filtri principali (LP, BP, HP). Deliyannis e Friend, nel 1975, presentarono una cella attiva biquadratica ad un solo operazionale, in grado di poter realizzare tutte o, almeno, le principali funzioni di ordine due.
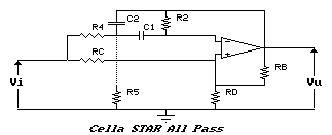
Questa cella prende il nome di Cella STAR, acronimo di Standard Tantalum Active Resonator, il nome è legato alla tecnologia con la quale vengono integrati i condensatori che vi compaiono. Talvolta essa prende anche il nome di SAB: Single Amplifier Biquad.
Il circuito della cella STAR è riportato in figura. Non
calcoleremo la funzione di trasferimento, di cui, comunque, si
daranno sia la forma che i coefficienti.
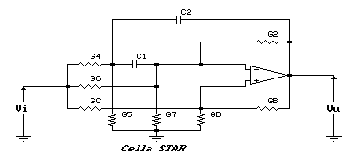
Osservando che sono state chiamate con G le conduttanze
delle singole resistenze, e ciò per praticità, scriviamo
la forma generale della funzione di trasferimento che si viene
ad ottenere:
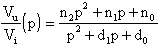
in cui i coefficienti sono:
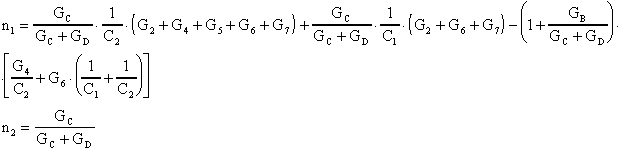
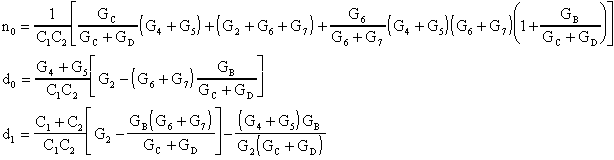
Si riportano, di seguito, i circuiti relativi ai filtri Passa
Alto di Notch, Passa Basso di Notch e Passa Tutto. Il calcolo
dei coefficienti della funzione di trasferimento è piuttosto
laborioso e lo si lascia al Lettore, riportando però i
risultati finali.
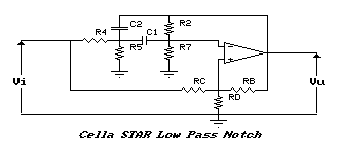
La funzione di trasferimento è del tipo:
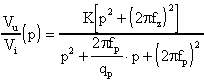
ed i coefficienti della funzione di trasferimento sono:
Con questi dati, i parametri caratteristici della cella Passa
Basso di Notch sono:
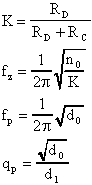
Per il filtro Passa Alto di Notch si avrà:
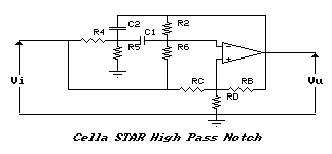
i coefficienti della F.d.T. sono:
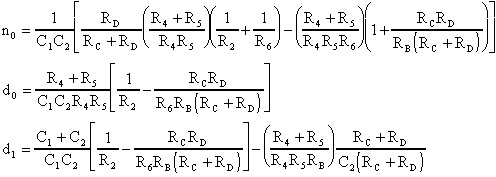
Con questi dati, i parametri caratteristici della cella Passa
Alto di Notch sono:
Per la cella Passa Tutto dovranno essere verificate le seguenti
relazioni:
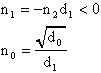
In base, però, alle relazioni scritte, è possibile
ridurre il circuito, eliminando R5 ed RB,
realizzando lo schema di figura:
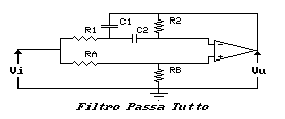
La funzione di trasferimento di questo circuito è la seguente:
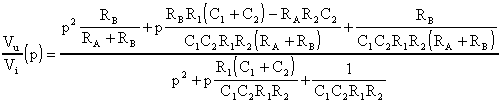
è facile vedere che, per realizzare un filtro Passa Tutto
e, quindi, per soddisfare le relazioni prima ricordate, deve essere
rispettato il rapporto:
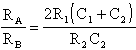
Anche per realizzare un filtro a Reiezione di Banda (Band Rejection), il cosìddetto "filtro notch" per eccellenza, esistono diverse soluzioni circuitali; fra tutte, ne analizzeremo due che differiscono sia per la topologia della rete, sia per i concetti che ne stanno alla base.
In primo luogo, l'idea è abbastanza banale: se da tutto
il segnale togliessimo solo una gamma di frequenze, otterremmo,
evidentemente, un filtro a reiezione di banda. Tenendo inoltre
conto del fatto che sottrarre un segnale da un altro è
pari a sommare i due segnali sfasandone uno di 180°, è
ovvio che mi basterà costruire un sommatore a cui far giungere
il segnale di ingresso ed il segnale che mi perviene da un filtro
passa banda invertente. Riunendo quanto detto in un circuito otteniamo
lo schema della figura seguente, nella quale è facile riconoscere
un filtro passa banda a reazioni multiple seguito da un sommatore
invertente.
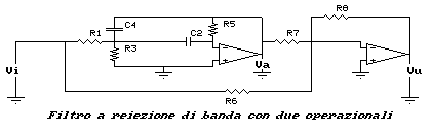
Per l'analisi di questo filtro basterà notare che, come
già visto, la funzione di trasferimento del filtro Passa
Banda fornisce:
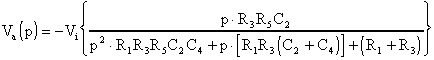
mentre l'analisi del circuito sommatore ci dà:
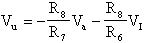
Il termine qp del filtro è evidentemente
dato dal filtro passa banda. Ponendo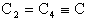 
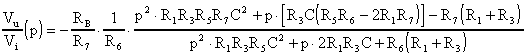
e
mettendo a sistema le due relazioni, otteniamo la funzione di
trasmissione del circuito:
Per far sì che la funzione sia quella di un filtro a reiezione
di banda, bisognerà garantire che il termine in p
a numeratore si annulli, quindi bisognerà soddisfare la
relazione: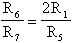 
.
I diagrammi di Bode in modulo e fase di un generico filtro di
questo tipo, sono riportati in figura.
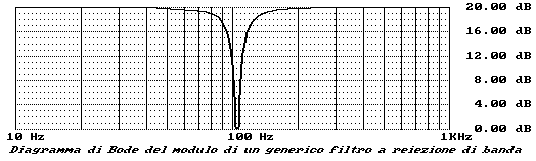
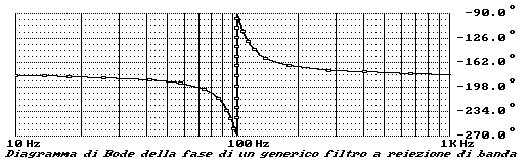
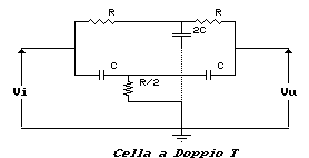
Il secondo metodo per realizzare un filtro a reiezione di banda fa leva sul fatto che è possibile costruire dei circuiti risonanti che si comportano, idealmente, come dei circuiti aperti, quindi aventi reiezione (o grado di annullamento) teoricamente infinito, alla frequenza di risonanza. Uno di questi circuiti è la cosiddetta "Cella a Doppio T" o Twin Tee. Basterà far precedere un normale amplificatore da questa cella per ottenere un filtro arresta banda.
La cella a doppio T è riportata in figura:
Il diagramma di Bode in modulo della stessa è il seguente:
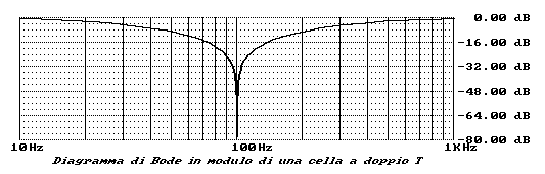
Esistono vari metodi di calcolo che ci permettono di ricavare
la funzione di trasferimento di questa cella, visibilmente simmetrica,
si possono, ad esempio, operare due trasformazioni stella-triangolo,
o, metodo più pratico, scrivere le equazioni ai nodi ed
impostare un sistema, nel nostro caso, di quattro equazioni in
quattro incognite. In ogni caso, la funzione di trasferimento
è la seguente:
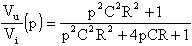
questa funzione ha un minimo in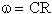 
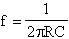
e quindi
la frequenza alla quale il filtro presenta la massima reiezione
è 
:
É evidente, a questo punto, la struttura topologica del
filtro a reiezione di banda:
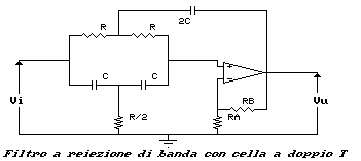
La funzione di trasferimento di questo filtro è:
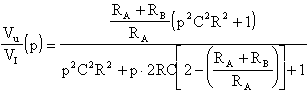
Osservando questa funzione salta all'occhio che il Q del filtro
è funzione del termine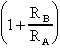 
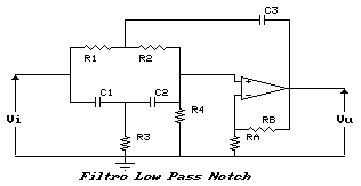
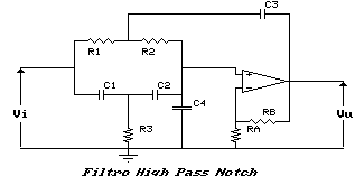
e che lo
stesso termine dovrà essere minore di 2 per garantire la
stabilità del circuito.
Esaminando la struttura del filtro a reiezione di banda appena
visto, ci accorgiamo che, inserendo un'opportuna ammettenza fra
il morsetto non invertente dell'operazionale e la massa, è
possibile rendere la frequenza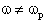
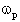
. Ciò
si trasforma, come abbiamo già visto, nel realizzare dei
filtri HPN o LPN. Nel caso in cui l'ammettenza sia una resistenza,
diventa minore di 
,
realizzando un filtro Passa Basso di Notch, se invece inserissimo
una capacità, otterremmo un Passa Alto di Notch. In ogni
caso, dovranno valere le relazioni 
ed
].
I circuiti che si ottengono sono riportati in figura.
Al termine di questo capitolo, che sicuramente non vuol essere
completo ma vuole, per altro, accarezzare i diversi tipi di filtri
attivi del secondo ordine, riportiamo di seguito i diagrammi di
Bode relativi ai filtri più significativi. Gli schemi degli
stessi sono quelli riportati nelle pagine precedenti ed i valori
dei componenti sono, rispettando gli eventuali rapporti indicati
nel testo, 15.92 nF per le capacità e 10 KW
per le resistenze.
