Appunti di TEORIA DELL’INFORMAZIONE
La formulazione si deve a Shannon e prende le mosse dall’osservazione che "La natura dell’informazione è discreta". Inizialmente si riteneva che il problema, nei sistemi di telecomunicazione, fosse quello di riprodurre fedelmente una funzione continua nel tempo. Invece, con Shannon, ci si accorse che, essendo l’informazione più limitata, era sufficiente trasmettere un insieme finito di dati per avere lo stesso contenuto informativo. Inoltre, e questo è il Secondo teorema fondamentale di Shannon, "ogni volta che elaboriamo dei dati, diminuiamo la quantità di informazione". Il problema che restava, comunque, aperto, era relativo all’interpretazione dell’informazione.
Secondo Shannon, il modello del sistema di comunicazione, è costituito da una Sorgente, da un Canale trasmissivo e da un Utente; in realtà, in precedenza, si faceva riferimento ad una modellizzazione più complessa del canale, si aveva, infatti, un modulatore, seguito da un mezzo trasmissivo (il canale) e da un ricevitore, costituito da un demodulatore. Inoltre, nella descrizione dei sistemi, si utilizzavano unità come l’energia
E, la banda W del canale, il tempo t (da notare che banda e tempo sono, in qualche modo, inversamente proporzionali, infatti, se è vero che con più tempo riesco a trasmettere più cose, è anche vero che per trasmettere la stessa informazione, o trasmetto più a lungo o allargo la banda). Con Shannon compare anche un quarto parametro: la complessità.Resta, ora, da valutare la bontà del sistema, quindi bisogna trovare un parametro che fornisca una sua quantificazione oggettiva.
Questa quantificazione è relativamente semplice nel caso di un Canale Binario Simmetrico [BSC]:

infatti può essere assunta a misura della bontà del sistema la probabilità di errore
a di ricevere un simbolo avendo trasmesso il suo negato. Ma se ci troviamo nel caso di un alfabeto più complesso, per ipotesi, l’alfabeto americano di ventisei simboli, può essere più difficile definire una misura della quantità di informazione. Proviamo, infatti, a considerare la lettera "u" che giunge dopo la "q". Nella lingua italiana, con la sola eccezione del termine "soqquadro", il fatto di avere una "u" dopo la "q" è un evento certo, quindi trasmettere un qualcosa che mi dica che dopo la "q" debba esserci una "u", vuol dire non trasmettere informazione. Da questo semplice ragionamento possiamo dedurre, quindi, che in un evento certo la quantità di informazione è nulla.Consideriamo, ora, un alfabeto discreto di n simboli, e tentiamo di associarvi una quantità di informazione. Sia, così, A = {a1, a2, ... aM} l’alfabeto di simboli ai , e sia I( ai ) la quantità di informazione. Ciascun simbolo è emesso con probabilità p{ai} = pi.
Caratterizziamo la probabilità mediante la variabile casuale
xM, per cui![]()
e che la sorgente sia stazionaria, cioè che: ![]() .
.
La quantità di informazione portata da un particolare simbolo dell’alfabeto, è strettamente correlata alla sua incertezza. Un aumento dell’incertezza, quindi, dovrebbe corrispondere a più informazione. É chiaro che il contenuto d’informazione dell’i-esimo simbolo, I(ai) sarà una funzione decrescente della sua probabilità, cioè ![]() se
se ![]() . Inoltre la misura dell’informazione associata ad ai, per essere realmente una misura dovrà essere sempre positiva, ovvero, I(ai)
. Inoltre la misura dell’informazione associata ad ai, per essere realmente una misura dovrà essere sempre positiva, ovvero, I(ai)
Vogliamo, inoltre, che la misura dell’informazione sia una funzione continua di pi, quindi I(ai) =
j(pi), in cui pi è una distribuzione di probabilità, quindi sottostante al fatto che pi ³ 0 e cheCon questi vincoli,
j(pi ,pj) = j(pi) + j(pj).Questa è un’equazione funzionale, che caratterizza la
j, di cui cerchiamo una soluzione.Si vede abbastanza chiaramente che la relazione che questa relazione è la proprietà del logaritmo: se
j(x,y) = j(x) + j(y), allora j(x) = K log (x).Questa è una soluzione ed è dimostrabile essere anche l’unica.
Accettando questi assiomi, l’unica misura dell’informazione che si può dare è, quindi, quella logaritmica. Da queste considerazioni discende che I(ai) =
j(pi) = K log(pi).Ricordiamo, per inciso, che la funzione logaritmica è una funzione convessa giù, il che, nel nostro caso, vuol dire che, avendo emesso dalla sorgente
xM, all’uscita del canale avremo hM ¹ xM , con diminuzione della quantità di informazione. É evidente che, tanto più il canale non perde informazione, tanto più è buono. Per esempio, l’errore tollerato nelle comunicazioni vocali è di 1 10-6. Inoltre, essendo pi una quantità compresa fra 0 e 1, K dovrà essere negativo, dovendo I(ai) essere maggiore di 0.Per rendere il tutto positivo, però, possiamo invertire l’argomento del logaritmo e stabilire una misura di informazione che soddisfi quanto asserito in precedenza. L’autoinformazione del messaggio ai sarà quindi:
![]()
La base a del logaritmo non è specificata. La sua scelta determina l’unità di misura assegnata al contenuto di informazione: se la base è "e" l’unità di misura sarà il NAT, se la base è "10" avremo l’HARTLEY, mentre se la base è "2" parleremo di BIT (acronimo di Binary Digit). L’uso del BIT si basa sul fatto che la corretta identificazione di uno fra due simboli egualmente simili comporta una quantità di informazione pari a :
![]()
Nella scienza dell’informazione si usa generalmente il NAT, in quanto, per via della derivata del logaritmo naturale, è più semplice da un punto di vista analitico; mentre, nell’ingegneria, prevale l’uso del Bit.
Appare evidente, dalla definizione, che se la probabilità di un simbolo è "1", allora la quantità dell’informazione è pari a 0 (risultato, comunque, atteso), mentre se la probabilità del simbolo è nulla, la quantità di informazione è infinita.
La definizione di quantità di informazione ci permette di associare ad ogni simbolo dell’alfabeto della sorgente il suo contenuto informativo. Una caratterizzazione dell’intero alfabeto può essere ottenuta definendo il contenuto medio di informazione di A:
![]()
La quantità ![]() è definita entropia dell’alfabeto della sorgente e viene misurata in Bit/Simbolo. Il termine entropia deriva dal fatto che questa quantità è massima quando le probabilità di emissione dei messaggi sono tutte uguali, ovvero quando i messaggi sono equiprobabili, in altri termini, l’entropia aumenta all’aumentare dell’incertezza sui messaggi che vengono emessi dalla sorgente stessa.
è definita entropia dell’alfabeto della sorgente e viene misurata in Bit/Simbolo. Il termine entropia deriva dal fatto che questa quantità è massima quando le probabilità di emissione dei messaggi sono tutte uguali, ovvero quando i messaggi sono equiprobabili, in altri termini, l’entropia aumenta all’aumentare dell’incertezza sui messaggi che vengono emessi dalla sorgente stessa.
Essendo l’entropia una media di positivi, allora H(A)
³ 0. Inoltre, essendo ![]() , ed essendo 0
, ed essendo 0
Ora, dire che ![]() significa che
significa che ![]() . Moltiplicando per 1 il log2M e ricordando che
. Moltiplicando per 1 il log2M e ricordando che ![]() posso dire che:
posso dire che: ![]() , quindi, per la proprietà distributiva,
, quindi, per la proprietà distributiva, ![]() da cui
da cui ![]() .
.
Soffermiamoci, per un inciso, sulla funzione logaritmo.
Questa è una funzione monotona crescente per ogni x fra 0 ed
¥, inoltre, è convessa giù. Ciò vuol dire che, considerando due punti qualunque ed unendoli con un segmento, questo sta sempre al di sotto della curva.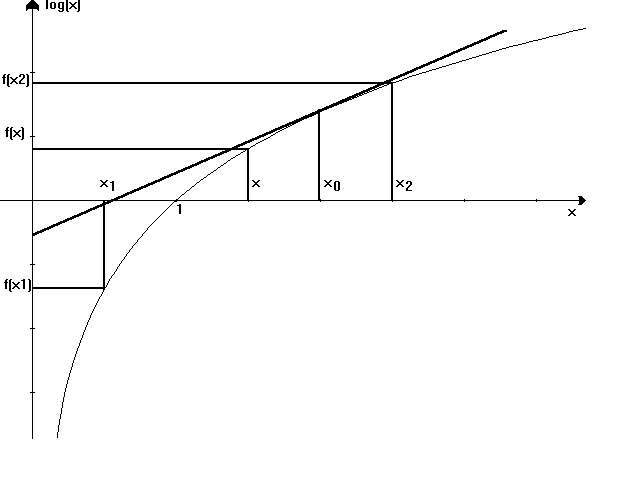
In generale, se consideriamo x1 < x < x2 ed
a compreso fra 0 ed 1, possiamo scrivere una combinazione lineare convessa x = ax1 + (1-a)x2 Þ x = x2 - a(x2 - x1). La combinazione prende il nome di "convessa" in quanto, combinando i due numeri, trovo un numero compreso fra i due; inoltre, per il Teorema di Talete, conoscendo f(x1) ed f(x2) = af(x1) + (1-a)f(x2), il punto che sta sul segmento è combinazione convessa degli estremi.L’ordinata che sta sulla curva è f(x), quindi
a
f(x1) + (1 - a) f(x2) £ f(x).Per le funzioni convesse si ha:
f(ax1 + (1 - a) x2) ³ af(x1) + (1 - a) f(x2).
Inoltre, se per un punto della curva convessa giù si traccia la tangente, la curva sta sempre sotto. Questa tangente ha equazione y = f(x0) + (x - x0) f’(x0), ma f(x) £ y quindi
f(x) £ f(x0) + (x - x0) f’(x0)
Se scegliessimo x0 = 1, allora
![]()

cioè log(x)
£ 0 + (x - 1)·(1/1). Da qui discende la relazione log(x) £ (x - 1).Tornando all’entropia, applicando questa disuguaglianza, possiamo dire che:
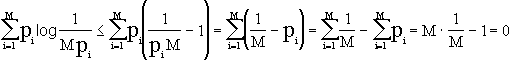
da cui
![]() . c.v.d.
. c.v.d.
Il massimo dell’entropia si ha quando i simboli sono equiprobabili e, essendo usasti nel modo più economico possibile, recano la massima quantità di informazione.
Pensiamo, ora, ad una sorgente che, anziché emettere un simbolo per volta, emetta una coppia di simboli con una data distribuzione di probabilità sulle coppie. Supponendo che gli alfabeti siano X ed Y, rispettivamente con simboli xi ed yi, per cui ![]() ed
ed ![]() , avremo coppie (xi yj).
, avremo coppie (xi yj).
Definendo p{xi yj} la probabilità della coppia (xi yj), cerchiamo l’entropia dell’alfabeto congiunto (joint entropy)
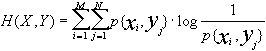 bit/simbolo
bit/simbolo
che misura il contenuto medio di informazione di una coppia di simboli di ingresso ed uscita, ovvero l’incertezza media del sistema di comunicazione formato dall’alfabeto d’ingresso, dal canale e dall’alfabeto di uscita considerati come un tutt’uno.
La relazione fra la quantità d’informazione dell’alfabeto congiunto e quella di x (o di y) è:
H(X,Y) £ H(X) + H(Y).
Vale la relazione di uguaglianza quando la p{xi,yj} = p{xi}·p{yj}, cioè quando gli alfabeti sono statisticamente indipendenti. Infatti possiamo dire che:
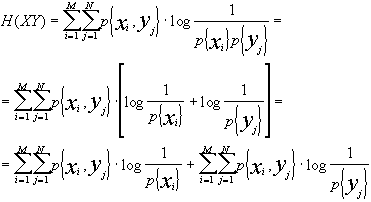
Possiamo fare alcune considerazioni: ricordiamo che, per il teorema della probabilità totale, avendo M eventi mutuamente esclusivi ed esaustivi, la probabilità di qualunque evento xi può essere espressa in ![]() e, analogamente,
e, analogamente, ![]() . In altri termini, si può notare che il logaritmo dipende solo da xi ed abbiamo una sommatoria doppia; se abbiamo una distribuzione di probabilità congiunta e sommiamo tutti gli elementi, abbiamo la probabilità marginale dell’altra variabile, appunto
. In altri termini, si può notare che il logaritmo dipende solo da xi ed abbiamo una sommatoria doppia; se abbiamo una distribuzione di probabilità congiunta e sommiamo tutti gli elementi, abbiamo la probabilità marginale dell’altra variabile, appunto![]() .
.
Da ciò discende che H(X,Y) = H(X) + H(Y) se e solo se X ed Y sono statisticamente indipendenti [c.v.d]
Resta, per altro, da dimostrare la disuguaglianza stretta.
Introduciamo, così, il concetto di entropia condizionale [ H(X|Y) ], che misura la quantità di informazione media necessaria per specificare il simbolo di ingresso x quando si conosca il simbolo y di uscita (o ricevuto), ovvero la quantità media di informazione necessaria a specificare il simbolo di uscita y quando sia noto il simbolo di ingresso x -[ H(Y|X) ]. Consideriamo, in questo caso, la prima, ovvero H(X|Y).
Ricordiamo che una distribuzione di probabilità condizionata p{xi|yj} è sempre una distribuzione di probabilità, per cui vale la relazione ![]() . Quindi, secondo la definizione, possiamo calcolare
. Quindi, secondo la definizione, possiamo calcolare
![]()
che mi fornisce l’entropia dei simboli xi sui simboli yj.
Possiamo, così, definire l’entropia condizionata dell’alfabeto X sull’alfabeto Y come:
![]()
che è la quantità di informazione mediata su tutti i simboli.
Cerchiamo, ora, la relazione fra H(X) ed H(X|Y).
Condizionare vuol dire fornire delle informazioni sui simboli e, quindi, ridurre la quantità di informazione che è necessario fornire; in altre parole ci si aspetta che l’entropia condizionata sia minore o, al limite, uguale a quella non condizionata, ovvero H(X)
³ H(X!Y). Dimostriamolo: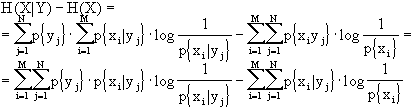
Ora, tra la probabilità condizionata, la probabilità dell’evento e la probabilità congiunta, vale la relazione:
p{xi,yj} = p{yj}·p{xi|yj}
inoltre, posso ricordare che la differenza di due sommatorie è pari alla sommatoria delle differenze. Da tutto ciò dirò che:
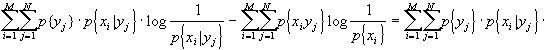
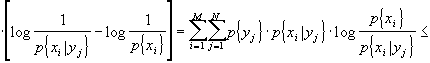 [ricordando che logx£x-1]
[ricordando che logx£x-1]
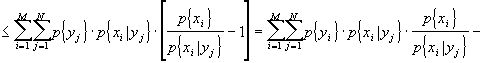
![]()
![]()
Bisogna, a questo punto, ricordare che:
![]() p{yj}·p{xi|yj}=p[xi,yj]
p{yj}·p{xi|yj}=p[xi,yj]
e che ![]() in quanto, essendo gli eventi statisticamente indipendenti, p{xi,yj}=p{xi}·p{yj} e, quindi,
in quanto, essendo gli eventi statisticamente indipendenti, p{xi,yj}=p{xi}·p{yj} e, quindi,
![]()
da cui
![]()
Con ciò, riprendendo i fili della dimostrazione, abbiamo verificato che H(x)
£ 0, quindi H(X|Y) - H(X) £ 0, ovvero H(X) ³ H(X|Y).É facilmente dimostrabile che H(XY) = H(Y) + H(X|Y) infatti:
![]()
ma, come abbiamo visto in precedenza, la probabilità congiunta è esprimibile come prodotto della probabilità condizionata per la probabilità dell’evento condizionante, quindi p{xiyj} = p{xi|yj}·p{yj}. Sostituendo, ottengo:
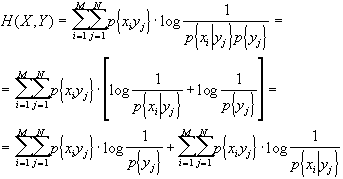
Ricordando, ora, che l’entropia condizionale H(X|Y) è esprimibile come
![]() e che, sempre per il Teorema della probabilità totale,
e che, sempre per il Teorema della probabilità totale,
![]() potrò scrivere:
potrò scrivere:
![]()
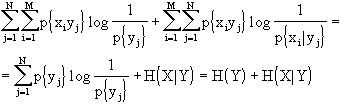
[q.e.d.]
Essendo H(X|Y) £ H(X) potrò, allora, dire che:
H(X,Y) = H(Y) + H(X|Y) £ H(Y) + H(X)
Calcoliamo, ora, l’entropia binaria, cioè l’entropia di un alfabeto con due simboli, che verrà indicata con H2(p):
![]()
Tracciandone il grafico, osserviamo che è simmetrica ed ha un massimo quando i due simboli sono equiprobabili, cioè per p=1-p=0.5, in cui H2(p) = log22 = 1 bit/simbolo. H2(p), quindi, decresce a zero sia per p
® 1 che per (1-p) ® 1. Nella letteratura, questa funzione viene anche detta W(p), o funzione a ferro di cavallo.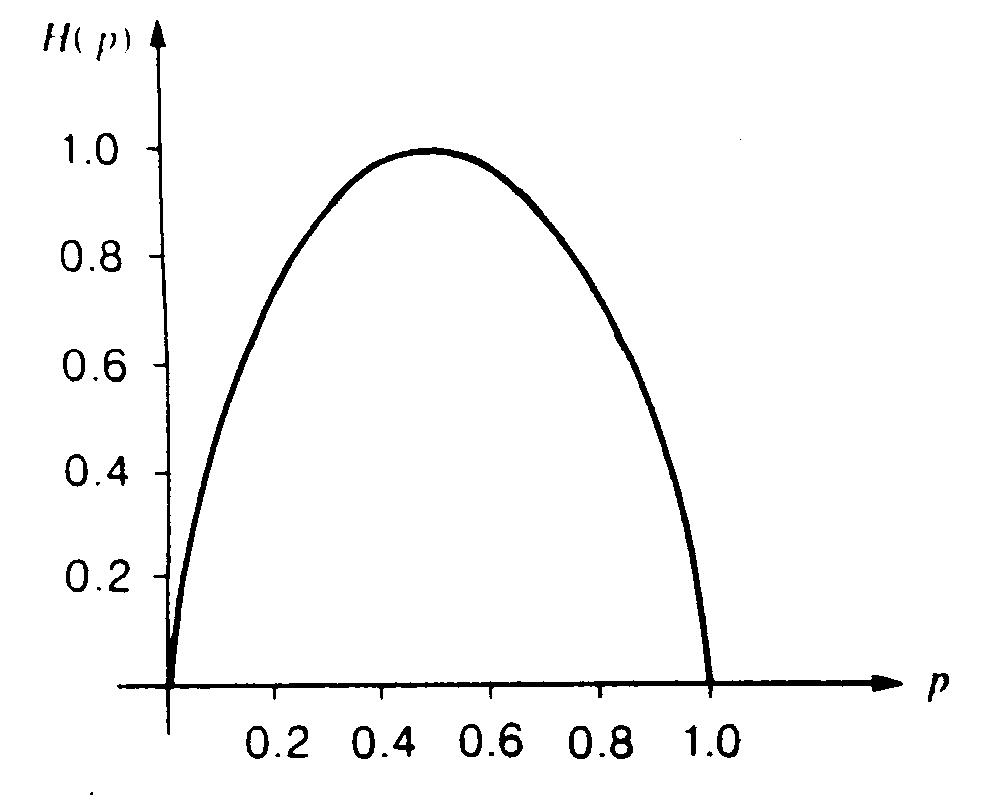
Facciamo, ora, l’esempio del segnale vocale, di un segnale, cioè, continuo. In teoria, se la variabile casuale diventa continua, bisogna fornire una quantità di informazione infinita perché possa essere quantificata, ovvero, dovremmo disporre di un sistema in grado di trasferire una quantità d’informazione infinita per poter trasmettere la variabile casuale. Ma, in realtà, non esiste un simile sistema. Ora, considerando che la quantità di informazione è finita, posso utilizzare un alfabeto finito e discreto; cioè, ed è il teorema di Shannon, comunque si realizzi un sistema di trasmissione, l’informazione utile è discreta.
Supponiamo, così, di disporre di un alfabeto A costituito dai numeri reali appartenenti all’intervallo [a,b], caratterizzato da una variabile
x che assuma valori in questo intervallo e da una funzione densità di probabilità da ritenersi continua, escludendo, quindi, i punti di discontinuità. Da quanto detto, possiamo ritenere continua fx(x).In altri termini, una sorgente di informazione continua, produce un segnale x(t) variante nel tempo. Tratteremo l’insieme di possibili segnali come un insieme di forme d’onda generate da qualche processo casuale, che si assume essere ergodico. In termini più pragmatici che formali, possiamo dire che il processo deve essere stazionario in senso lato e che un suo campionamento tipico contiene tutte le variazioni statistiche del processo. Inoltre assumiamo che il processo abbia larghezza di banda finita, nel senso che x(t) è completamente caratterizzato in termini di valori campionati periodicamente. Così, ad ogni istante di campionamento, l’insieme dei possibili valori campionati costituisce una variabile casuale continua descritta dalla sua funzione densità di probabilità.
La quantità media d’informazione per valore campionato di x(t) è misurata dalla funzione entropia:
![]()
Questa relazione, comunque, è una misura d’informazione relativa e non assoluta. L’entropia assoluta di una sorgente continua può essere definita dal ragionamento seguente.
Costruiamo una successione di variabili casuali
xN , con N®¥ , supponendo che sia proprio N il numero di valori che xN può assumere. Per semplicità, consideriamo tre intervalli; in questo caso possiamo definire un intervallo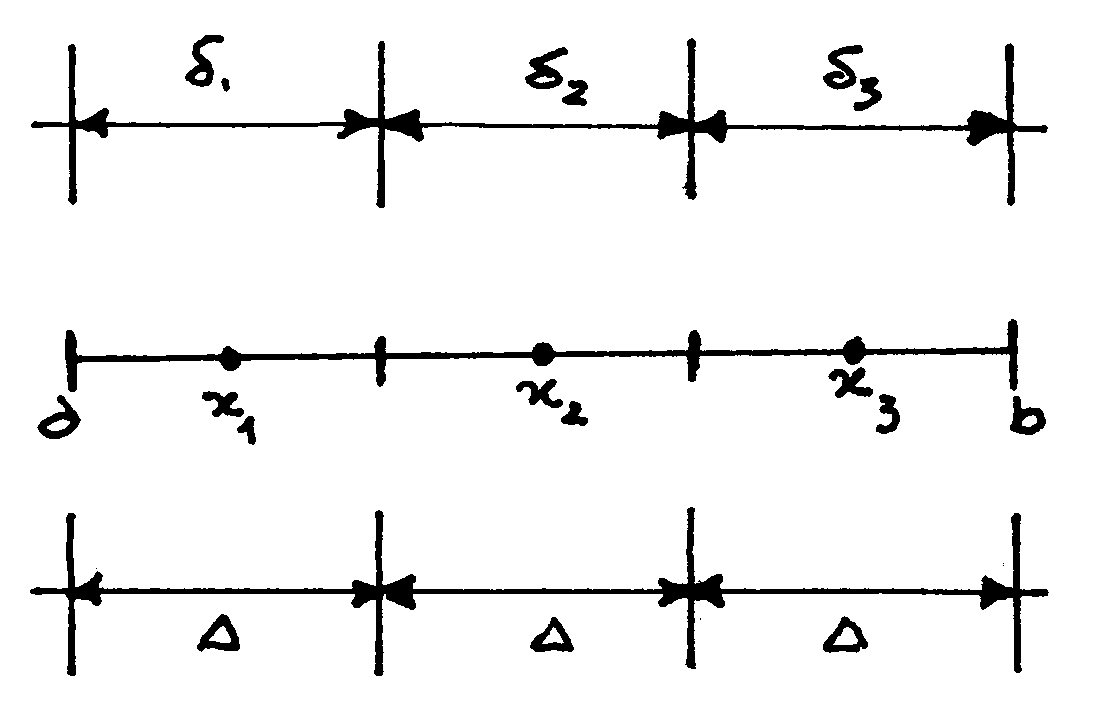
Dirò che ![]() . Così facendo, in realtà, associo alla variabile casuale continua una variabile casuale discreta.
. Così facendo, in realtà, associo alla variabile casuale continua una variabile casuale discreta.
Per la definizione di probabilità di eventi della funzione densità di probabilità ho che ![]() quindi
quindi ![]() .
.
Essendo continua la funzione densità di probabilità, posso applicare il teorema della media integrale:
![]()
A questo punto, posso dire che ![]() , ricordiamo che
, ricordiamo che ![]() e, quindi
e, quindi ![]() .
.
Riducendo gli intervalli, facciamo tendere N
® ¥ dicendo cheSeguendo la catena di uguaglianze appena vista, per cui
![]()
e, sostituendo, posso dire che:
![]()
![]() .
.
Essendo ![]() ed essendo
ed essendo ![]() , allora
, allora ![]() . Quindi
. Quindi
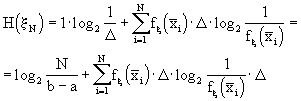
Prendiamo, adesso, il![]() ricordando che, in questo caso, il limite di una somma è pari alla somma dei limiti e rammentando anche la definizione di integrale secondo Riemann, potremo dire che:
ricordando che, in questo caso, il limite di una somma è pari alla somma dei limiti e rammentando anche la definizione di integrale secondo Riemann, potremo dire che:
il secondo termine può ricordare un’entropia, ed è per questo che lo si definisce entropia differenziale che viene indicata con:
![]()
ma, in realtà, non è una misura, in quanto ![]() può assumere anche valori negativi o nulli.
può assumere anche valori negativi o nulli.
Inoltre, l’entropia differenziale di una variabile casuale uniforme è nulla, ma la variabile casuale uniforme porta informazione.
Scriverò così che:
![]()
ma il primo termine è, palesemente, infinito, mentre il secondo resta finito. Quindi, per una variabile casuale continua, la misura della quantità d’informazione è infinita.
In senso pratico, posso infatti dire che, per specificare un numero reale, ho bisogno di infinite cifre decimali, ognuna recante la propria informazione.
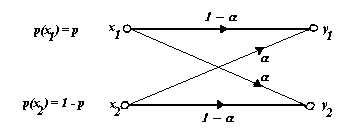
Vediamo, ora, una descrizione del canale.
Un canale discreto e caratterizzato da un alfabeto di ingresso ![]() , da un alfabeto di uscita
, da un alfabeto di uscita ![]() e da un insieme di probabilità condizionate
e da un insieme di probabilità condizionate ![]() che rappresenta la probabilità di ricevere il simbolo yj avendo trasmesso il simbolo xi. Inoltre si assume che il canale sia senza memoria, e ciò significa che
che rappresenta la probabilità di ricevere il simbolo yj avendo trasmesso il simbolo xi. Inoltre si assume che il canale sia senza memoria, e ciò significa che
![]()
in cui x1, x2, ... ,xn e y1, y2, ... , yn rappresentano, rispettivamente, n simboli trasmessi e ricevuti.
Per "disegnare" il canale discreto senza memoria, si usa una rappresentazione a grafo bipartito di questo tipo:
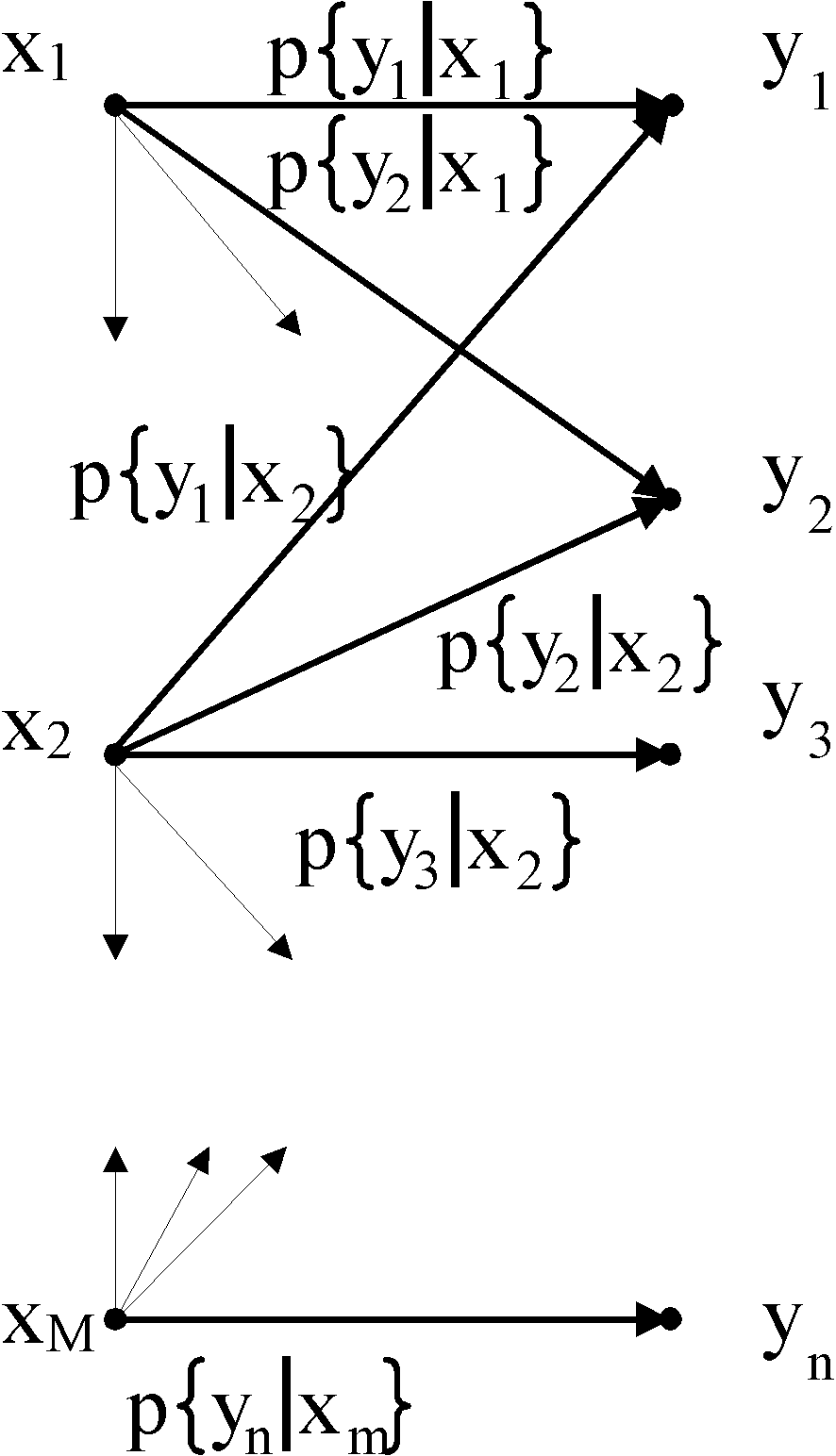
Ogni freccia rappresenta una transizione da uno dei simboli dell’alfabeto di ingresso ad uno dei simboli dell’alfabeto di uscita, ed è etichettata con la probabilità condizionale della transizione. Evidentemente la somma delle probabilità relative a tutte le frecce dello stesso simbolo è pari ad 1. È parimenti evidente che, conoscendo la distribuzione di probabilità sui simboli di ingresso p{xi} e la caratterizzazione del canale p{yj|xi} possiamo facilmente conoscere anche la distribuzione di probabilità in uscita. Infatti, per il teorema della probabilità totale,
![]()
Si è soliti sistemare le probabilità condizionate p{yj|xi} nella matrice di canale.
La matrice di canale è costruita in modo tale che il primo pedice (le righe) sia relativo all’ingresso, mentre il secondo (le colonne) sia relativo alle uscite. Per cui
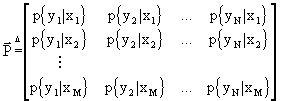
In questa matrice, essendo le ![]() delle probabilità, è evidente che ogni elemento avrà valore compreso fra 0 ed 1. Inoltre, per lo stesso motivo,
delle probabilità, è evidente che ogni elemento avrà valore compreso fra 0 ed 1. Inoltre, per lo stesso motivo, ![]() . In altri termini, la somma degli elementi di una riga vale 1. Se si verifica anche che
. In altri termini, la somma degli elementi di una riga vale 1. Se si verifica anche che ![]() , cioè se anche la somma degli elementi delle colonne vale 1, allora la matrice si dice doppiamente stocastica.
, cioè se anche la somma degli elementi delle colonne vale 1, allora la matrice si dice doppiamente stocastica.
Analizziamo, a questo punto, la quantità più importante introdotta da Shannon, cercando di rispondere alla domanda "In un canale di trasmissione discreto e senza memoria, quanta informazione danno i simboli ricevuti sui simboli trasmessi ?" cioè, quanto vale I(X,Y) ? Ora, parte dell’informazione H(X) trasmessa sul canale, è persa a causa del rumore presente sul canale stesso. Questa parte è misurata tramite "l’equivocazione" di canale H(X|Y). Il termine equivocazione sembra appropriato se si osserva che per un canale privo di rumore H(X|Y)=0, in quanto il simbolo ricevuto determina univocamente quello trasmesso, mentre, per un canale inutile, quello, cioè, in cui i simboli di uscita sono indipendenti da quelli d’ingresso ( p{yj|xi} = p{yj} ), H(X|Y) = H(X). Sembra, così, logico definire un’informazione mutua, che, in letteratura, prende, meno correttamente, il nome di "flusso medio di informazione", come:
![]() bit/simbolo
bit/simbolo
Ricordando che H(X,Y) = H(Y,X) = H(X) + H(Y|X) = H(Y) + H(X|Y), possiamo derivare un’altra forma per la stessa quantità:
![]() .
.
Confrontando le due formule, è facile dimostrare che
![]()
Dalla definizione si vede, anche, l’entropia come capacità potenziale di un alfabeto di fornire informazione.
Se il legame fra X ed Y è deterministico, allora I(XY) = 0. Infatti, se i simboli dell’alfabeto di ingresso sono in corrispondenza "uno a uno" con quelli dell’alfabeto di uscita, [p{x|y} = 1
" x=y o x=f(y) e p{x|y} = 0 " x ¹ y altrimenti ] allora è evidente che p{x|y} = p{x}, da cui H{X|Y} = H{X} e, ricordando la definizione di informazione mutua, I(X:Y) º H(X) - H(X|Y) = 0.Possiamo soffermarci su alcune proprietà della mutua informazione.
Sostituendo nella definizione ottengo:
![]()
Torniamo al caso del canale simmetrico binario:
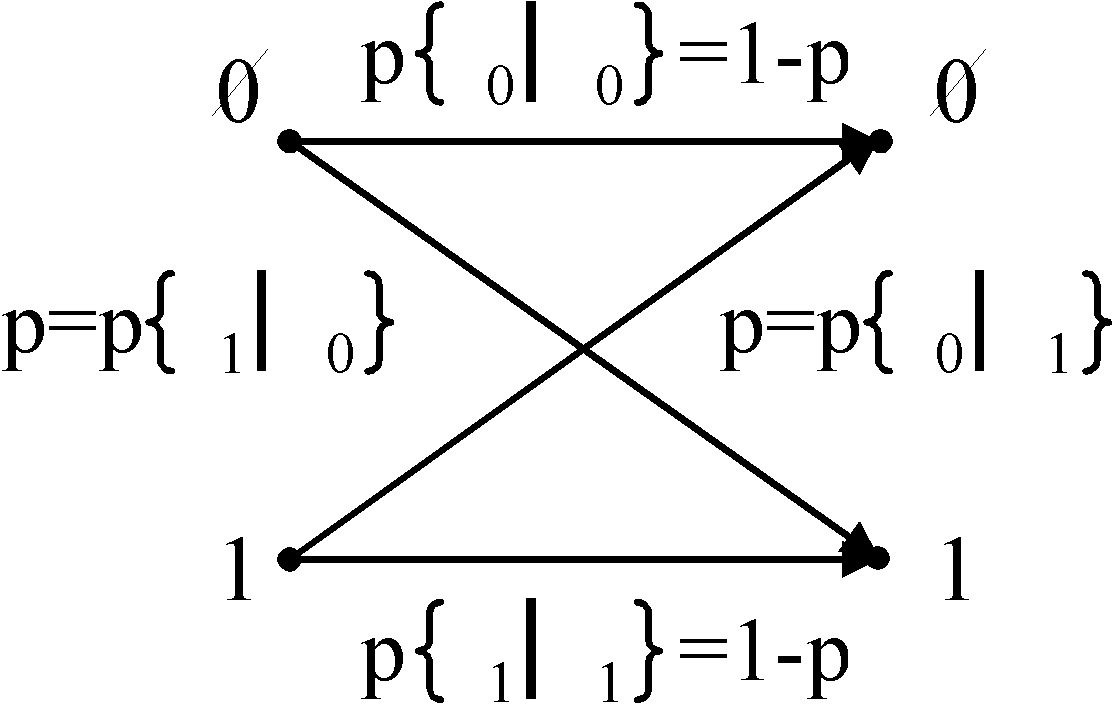
la matrice stocastica sarà:
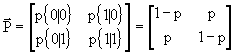
Vogliamo calcolare la mutua informazione:

Prima di continuare, riprendiamo alcuni punti della teoria delle probabilità. Innanzitutto, per definizione di probabilità congiunta, posso dire che:
![]()
Dalla definizione di probabilità condizionata:
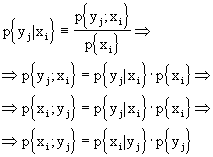
Riscriviamo, inoltre, il teorema della probabilità totale:
![]()
Riprendiamo il teorema di Bayes e facciamo alcune considerazioni:
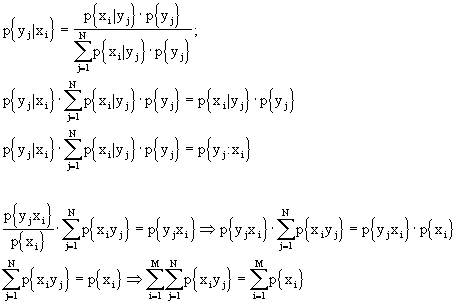
e ciò significa che, avendo la distribuzione di probabilità congiunta, possiamo calcolare le distribuzioni di probabilità marginali come sommatoria delle distribuzioni di probabilità congiunte, fatta sull’altro indice.
Torniamo sulla mutua informazione e sfruttiamo i risultati ottenuti:
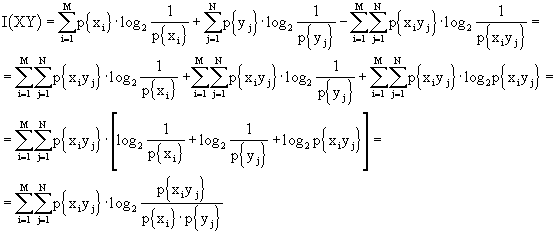
Da questa equazione si nota la simmetria dei due alfabeti.
Se, ora, osserviamo che ![]() e ricordando il già citato teorema della probabilità totale, posso dire, sfruttando il risultato appena raggiunto, che
e ricordando il già citato teorema della probabilità totale, posso dire, sfruttando il risultato appena raggiunto, che
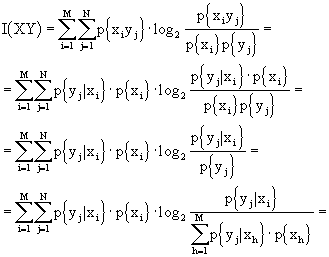
Questa notazione esprime la mutua informazione in funzione delle probabilità condizionate.
Definiamo ora la capacità di Shannon, tentativo di parametrizzare l’ottimizzazione dell’uso di un canale di caratteristiche note. Infatti, osservando che la mutua informazione è:
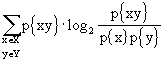 ,
,
vediamo che l’unica variabile libera è la distribuzione di probabilità dell’alfabeto di ingresso. Facciamo, allora, variare il vettore degli ingressi in modo da massimalizzare l’informazione mutua e definiamo "capacità" di un canale discreto senza memoria il massimo della mutua informazione I(X;Y) che può essere trasmesso sul canale. Riprendendo la scrittura vista in precedenza che, per inciso, discende dalla relazione I(X;Y) = H(Y) - H(Y|X), diciamo che
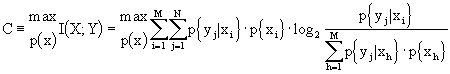
con ![]() .
.
Il significato parrebbe non essere molto chiaro, ma in realtà fa riferimento al teorema fondamentale di Shannon sulla codifica del segnale.
Vedremo, in seguito, che non è possibile una trasmissione efficace sul canale se il numero di bit per simbolo è maggiore della capacità del canale.
Di fatto, oggi, si sceglie il canale in modo non da minimizzare la probabilità di errore, quanto di massimizzare la capacità. Infatti, sebbene ci siano linee di pensiero differenti, si ritiene che quanto più sia alta C, tanto più alta sarà la velocità di trasmissione. Si dimostrerà che, se la quantità di informazione di sorgente è minore della velocità, allora è possibile costruire un canale con probabilità di errore nulla.
Consideriamo un canale che, per semplicità, sarà supposto binario, di capacità C. Poniamo, all’ingresso del canale, un codificatore e, in uscita, un decodificatore. Siano i simboli usati affetti da una probabilità di errore p che va ridotta. Per raggiungere questo scopo, tradizionalmente, si usava un codice a ripetizione. Ad esempio, il codificatore aggiungeva due simboli identici; così facendo, partivano tre simboli uguali. In ricezione potevo, così, avere 23=8 possibilità. La regola di decodifica era, a questo punto, ragionevolmente basata sul peso. Con questo meccanismo, riducevo sì la probabilità di errore dei simboli di sorgente, ma, in realtà, rallentavo la trasmissione ad 1/3. Usando direttamente il canale, la probabilità di errore sarebbe stata p, mentre ora ho una probabilità pari a [1- (probabilità di corretta ricezione)].
Il ragionamento è banale, se ricevo le parole 000 o 111 so di avere probabilità di errore pari a 0, per i simboli intermedi deciderò sul numero maggiore di simboli uguali.
Traducendo in formule il discorso, dirò che:
![]() .
.
In pratica, col codice a ripetizione, distribuivo su ogni bit la probabilità di errore, riducendo, di fatto, le probabilità.
Ora, se riesco a trovare una regola di codifica tale che la quantità di informazione sia minore della capacità, allora deve esistere una regola di codifica tale che la probabilità di errore possa essere resa piccola a piacere.
Soffermiamoci momentaneamente su questo discorso, abbozzando dei concetti su cui torneremo più dettagliatamente in seguito.
Abbiamo detto, definendo l’entropia di sorgente, che la quantità di informazione prodotta dalla sorgente in un arbitrario intervallo simbolico è una variabile casuale discreta con valori possibili pari a I1,I2,...,IM. L’informazione per simbolo attesa è, allora, data dalla media statistica, quindi:
![]() bits/simbolo
bits/simbolo
questa quantità, come visto, è l’entropia. Possiamo interpretare questa definizione in modo più pragmatico, osservando che quando la sorgente emette una sequenza di n simboli, con n"1, l’informazione totale che viene trasferita è di circa n·H(X) bits. Siccome la sorgente produce r simboli al secondo, la durata temporale di questa sequenza è n/r. Allora l’informazione dovrà essere trasferita al ritmo medio di 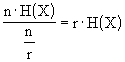 bits/secondo. Formalmente, definiamo il tasso di informazione di sorgente [Source Information rate] come
bits/secondo. Formalmente, definiamo il tasso di informazione di sorgente [Source Information rate] come ![]() bits/secondo, che è, quindi, una quantità critica relativamente alla trasmissione.
bits/secondo, che è, quindi, una quantità critica relativamente alla trasmissione.
Shannon ha asserito che l’informazione da qualsiasi sorgente discreta senza memoria può essere codificata come bit e trasmessa su un canale privo di rumore al passo di segnale ![]() binits/sec [il "binit" si usa al posta di "bit" nei messaggi o negli elementi di codifica].
binits/sec [il "binit" si usa al posta di "bit" nei messaggi o negli elementi di codifica].
Ora, un canale, normalmente, ha alfabeti di sorgente e di utente definiti e caratterizzati dalle probabilità dirette di transizione, così che, come abbiamo visto, le uniche quantità variabili in I(X;Y) sono le probabilità di sorgente p{xi}. Di conseguenza, il massimo trasferimento di informazione richiede specifiche statistiche di sorgente. Questo massimo è, come ormai noto, la capacità di canale: massima quantità di informazione trasferita per simbolo di canale. Possiamo anche misurare la capacità in termini di tasso di informazione: se S è il massimo tasso simbolico permesso dal canale, allora la capacità per unità di tempo è C’ = S·C [bits/sec] che rappresenta il massimo tasso di trasferimento di informazione.
Vediamo, così, che vi è un intimo legame fra entropia, informazione, mutua informazione, tasso di informazione e capacità del canale.
Riorganizzando il ragionamento, possiamo asserire che:
"Se un canale ha capacità C ed una sorgente ha tasso d’informazione R £ C, allora esiste un sistema di codifica tale che l’uscita della sorgente può essere trasmessa sul canale con frequenza di errore piccola a piacere. Viceversa se R > C, allora non è possibile trasmettere l’informazione senza errori."
Questa è l’enunciazione del Teorema Fondamentale di Shannon per un canale rumoroso. Torneremo in seguito, e più dettagliatamente, su questi concetti. Per il momento, ci basti pensare che il costo da pagare per inviare un segnale con probabilità di errore piccola a piacere è la complessità dei sistemi di codifica e di decodifica. Se decidessimo di trasmettere una quantià di informazione superiore alla capacità di Shannon, allora la probabilità di errore avrebbe un minimo non nullo.
Un esempio di codice, usato da Shannon, è il codice Hamming, codice a blocchi lineare (n,k) con q ³ 3 bits di controllo, in cui ![]() e
e ![]() . Facciamo l’esempio in cui q=3 e, quindi, n=7 e K=4.
. Facciamo l’esempio in cui q=3 e, quindi, n=7 e K=4.
Senza addentrarci sulla generazione dei codici a blocchi, ci basti sapere che, nel caso di codice Hamming (7,4), si trasmettono i 4 simboli xi più 3 simboli di parità yi generati secondo questa regola:

Riportiamo di seguito il codice così generato, col peso di ogni parola di codice. Si noti che a parole di parità uguali, corrispondono pesi di parola differenti.
0000 000 0
0001 011 3
0010 110 3
0011 101 4
0100 111 4
0101 100 3
0110 001 3
0111 010 4
1000 101 3
1001 110 4
1010 011 4
1011 000 3
1100 010 3
1101 001 4
1110 100 4
1111 111 7
La probabilità sarà, quindi, ![]() . Costruendo un codice che mantenga costante il rapporto 4/7, come 8/14, 12/21, 16/28, ecc., potrò minimizzare la probabilità di errore senza variare la capacità, in quanto avrò scelto C>0.571, ma se ciò non fosse, non potrò mai riuscire a ridurre la probabilità di errore.
. Costruendo un codice che mantenga costante il rapporto 4/7, come 8/14, 12/21, 16/28, ecc., potrò minimizzare la probabilità di errore senza variare la capacità, in quanto avrò scelto C>0.571, ma se ciò non fosse, non potrò mai riuscire a ridurre la probabilità di errore.
Apriamo, ora, un piccolo inciso sul calcolo dei massimi e dei minimi vincolati.
Sia R uno spazio funzionale normo-lineare. Si assuma che sia data una regola che associ un numero complesso
j(f) ad ogni funzione f Î R. Si definisce j funzionale su R.Se j è un funzionale su R, ed f,h Î R, allora il funzionale
![]()
è chiamato differenziale di Fréchet di
j. Il concetto di differenziale di Fréchet fornisce una regola per calcolare i massimi ed i minimi di un funzionale. Abbiamo il seguente risultato: una condizione necessaria perché j(f) raggiunga un valore massimo o minimo per f=f0 è che dj(f0;h)=0 " hÎR.In molti problemi di ottimizzazione si richiede la funzione ottima per soddisfare certi vincoli. Consideriamo, in particolare, la situazione in cui un funzionale
j su R debba essere ottimizzato sotto n vincoli dati in forma implicita y1[f]=C1, y2[f]=C2,...,yn[f]=Cn, in cui y1, y2,...,yn siano funzionali su R, e C1, C2,...,Cn siano costanti. Abbiamo che, se f0ÎR fornisce un massimo o un minimo di j soggetto ai vincoli yi[f]=Ci, con 1£ i £ n, e se gli n funzionali dyi[f0;h] sono linearmente indipendenti, allora ci sono n scalari l1, l2, ... , ln che fanno sì che i differenziali di Fréchet di Questo risultato fornisce una regola per il calcolo di massimi e minimi vincolati. Il procedimento consiste nel formare il funzionale ![]() , calcolare il suo differenziale di Fréchet e trovare le funzioni f che lo annullano per ogni h. I valori dei "moltiplicatori di Lagrange" l1, l2, ... , ln possono essere calcolati utilizzando le equazioni vincolanti.
, calcolare il suo differenziale di Fréchet e trovare le funzioni f che lo annullano per ogni h. I valori dei "moltiplicatori di Lagrange" l1, l2, ... , ln possono essere calcolati utilizzando le equazioni vincolanti.
Per meglio illustrare il metodo, risolviamo un semplice problema.
Sia da trovare la relazione che fornisce fra gli infiniti rettangoli di lati x ed y, quello di area massima, sotto il vincolo che x+y=p.
La relazione sarà: ![]() .
.
Massimizziamo la Lagrangiana L come se non ci fossero i vincoli:
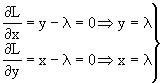 sostituisco nel vincolo
sostituisco nel vincolo ![]() da cui
da cui ![]() .
.
Pertanto i valori di x e di y che risolvono il problema sono ![]() ed
ed ![]() .
.
Con questo metodo cerchiamo un massimo per la quantità:
![]()
col vincolo che ![]() e che
e che ![]() .
.
La lagrangiana sarà: ![]() . Cerchiamo quando
. Cerchiamo quando ![]() .
.
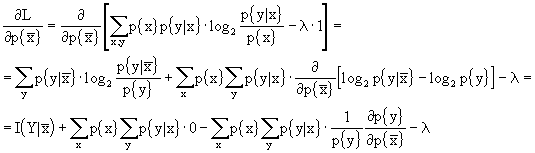
Ricordando che ![]() da cui
da cui ![]() , posso dire che
, posso dire che
![]()
Ricordando la definizione di probabilità condizionata, sostituisco a
![]() per cui:
per cui:
![]() ma
ma
![]() per cui
per cui
![]() .
.
Se il canale è simmetrico e tutte le variabili sono usate con la stessa probabilità, questa funzione è massimizzata, quindi la capacità è raggiunta.
La definizione di "simmetria" discende dall’analisi della matrice stocastica: un canale è simmetrico in senso stretto se tutte le righe della matrice sono permutazioni della prima riga e se tutte le colonne sono permutazioni della prima colonna. In questo caso, la somma degli elementi di una riga (probabilità di ingresso) è pari ad 1, mentre le probabilità di uscita sono uguali, ciò sta ad indicare che, se gli ingressi sono equiprobabili, tali sono anche le uscite.
Continuando con la definizione, diremo che un canale è simmetrico in senso lato se la matrice può essere ripartita in sottomatrici o, se si preferisce, in sottoinsiemi di colonne tali che ciascun sottoinsieme goda della proprietà dei canali simmetrici in senso stretto.
Se gli ingressi sono equiprobabili, quindi se ![]() , allora I(Y|x) non dipende da x e la capacità del canale è raggiunta.
, allora I(Y|x) non dipende da x e la capacità del canale è raggiunta.
Torniamo al computo della capacità. Dicevamo che
![]() , ma
, ma
![]() per cui
per cui ![]() .
.
Se il canale è simmetrico, essendo I(Y|x) costante e pari a I(Y|x) = l + 1, avremo
![]()
In questo caso basterà calcolare I(Y|x).
Nel caso in cui gli ingressi siano equiprobabili, I(Y|x) non dipende da x, infatti abbiamo:
![]() .
.
Avevamo detto che ![]() , ma
, ma ![]() essendo equiprobabili, quindi
essendo equiprobabili, quindi
![]() .
.
Se il canale è strettamente simmetrico, tutte le colonne, tutte le colonne sono permutazioni della prima colonna, quindi la somma di tutti gli elementi non dipende dalla colonna, e potremo dire, quindi, che ![]() costante, per cui
costante, per cui
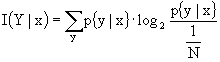 .
.
Un esempio aiuterà a capire il concetto.
Supponiamo di avere questa matrice di transizione:
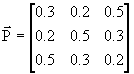 .
.
Il canale è simmetrico in senso stretto: le righe sono permutazioni della prima riga e le colonne lo sono della prima colonna infatti, sommando per righe (relative agli ingressi) abbiamo sempre 1, così come sommando gli elementi delle colonne, per cui ![]() e
e ![]() .
.
Calcoliamo 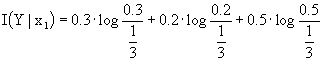 . Otteniamo che:
. Otteniamo che:
![]() . Il valore è, come si può notare, indipendente da x, è massimo ed è pari alla capacità del canale.
. Il valore è, come si può notare, indipendente da x, è massimo ed è pari alla capacità del canale.
Come altro esempio, calcoliamo la capacità del canale simmetrico binario, per il quale le probabilità dei simboli in ingresso siano, in questo caso, p{0}=0.5 e p{1}=0.5; in uscita avremo p’{0}=0.5 e p’{1}=0.5.
Il canale ha matrice stocastica pari a:
![]() .
.
Vogliamo calcolare la capacità. Possiamo muoverci in due modi:
Considerando che i simboli sono equiprobabili in ingresso ed in uscita, e quindi ![]() ,
, ![]() e
e ![]() , e che il canale e simmetrico, potremo dire che:
, e che il canale e simmetrico, potremo dire che:

Potevamo raggiungere lo stesso risultato per altra via: abbiamo visto che I(X;Y) = H(Y) – H(Y|X) ed abbiamo anche detto che una proprietà importante del canale simmetrico è che H(Y|X) è indipendente dalle probabilità di ingresso p{xi} e dipende solo dalla matrice di canale ![]() . Infatti:
. Infatti:
![]() , essendo
, essendo
![]() , quindi
, quindi
![]() .
.
Possiamo fare due osservazioni:
![]() quindi
quindi
![]()
Possiamo diagrammare la capacità del canale binario simmetrico in funzione di p:
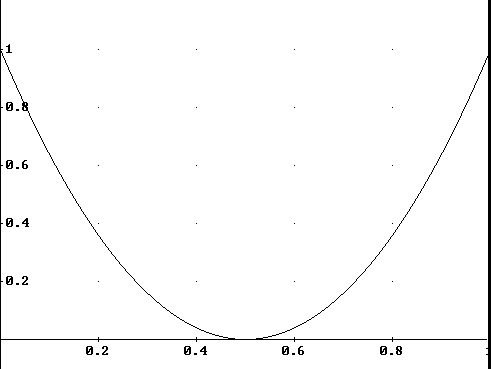
Si può notare che la capacità è massima quando p=0 o p=1, infatti entrambe queste situazioni conducono al canale senza rumore, in cui ![]() ed in cui H(X|Y) = H(Y|X) = 0 e H(X,Y) = H(X) = H(Y).
ed in cui H(X|Y) = H(Y|X) = 0 e H(X,Y) = H(X) = H(Y).
Per p=0.5, invece, la capacità è nulla in quanto i simboli di uscita sono indipendenti dai simboli di ingresso e nessuna informazione può fluire nel canale, che degenera nel canale inutile, in cui p{yj|xi} = p{yj}
" j,i. In questo caso la matriceConsideriamo, in questa piccola rassegna di esempi, il canale simmetrico con cancellazione (o BEC: Binary Erasure Channel).

Sia p la probabilità di errore e q la probabilità di cancellazione; la matrice stocastica sarà:
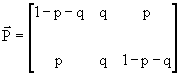
Da questa matrice vediamo che il canale non è simmetrico in senso stretto, ma lo è in senso lato, in quanto la matrice può essere ripartita in due sottoinsiemi di colonne, tali che ogni sottoinsieme goda delle proprietà dei canali simmetrici. Infatti, scambiando la colonna di posto 3 con quella di posto 2, otteniamo:
![]()
Con questo risultato, della cui utilità pratica ci accorgeremo ben presto, abbiamo dimostrato che il BEC è simmetrico in senso lato, quindi le probabilità di uscita possono essere diverse. Nei canali simmetrici in senso stretto, invece, le uscite sono equiprobabili.
Per calcolare la capacità, dobbiamo calcolare ![]() , dato che il canale è simmetrico. Valutiamo, pertanto,
, dato che il canale è simmetrico. Valutiamo, pertanto, ![]() , essendo gli ingressi equiprobabili.
, essendo gli ingressi equiprobabili.
Con riferimento alla matrice delle probabilità di transizione, possiamo dire che basterà sommare per colonne e dividere per M, infatti:
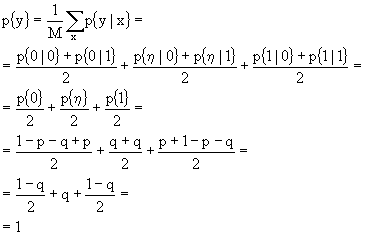
La capacità sarà:

in cui con H2(•) si è indicata l'entropia binaria. Basta ricordare che ![]() .
.
È facile osservare che, sostituendo al posto di ![]() e, quindi,
e, quindi, ![]() , effettivamente il risultato ottenuto è corretto.
, effettivamente il risultato ottenuto è corretto.
Se p=0, allora C=1-q.
Si può giungere allo stesso risultato per altra via.
Sfruttando le proprietà dei canali simmetrici in senso lato e, quindi, dividendo, come visto, la matrice stocastica in due sottomatrici, cioè:
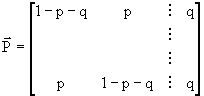
e normalizzando la prima matrice per avere la somma degli elementi delle righe pari ad 1, scriveremo:

Si può dimostrare che la capacità è la media, secondo queste probabilità di scelta, della capacità di tutti i canali che, a questo punto, sono simmetrici in senso stretto, cioè:
![]()
In questo caso la capacità è pari al prodotto del termine normalizzante per la capacità di un canale simmetrico binario, per cui:
![]()
in cui 0 è la capacità di un canale con un ingresso e due uscite.
Più in generale, è dimostrabile che la capacità di un canale simmetrico in senso stretto è pari a:
C = log2(N° di Uscite) - H(Probabilità di Transizione della Riga 1)
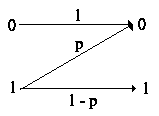
Un altro tipo di canale, usato per rappresentare soprattutto le comunicazioni magnetiche ed in fibra ottica, è il canale z, non simmetrico, e ciò perché, trasmettendo, ad esempio, fotoni, è impossibile che in assenza di luce trasmessa, questa venga ricevuta. La modellizzazione grafica è la seguente:
con p si indica la probabilità di errore, cioè, per proseguire nell'esempio, che, trasmettendo luce, questa venga assorbita nel canale e non raggiunga l'uscita.
Calcoliamo la capacità.
La matrice di transizione sarà: ![]() ; da questa è evidente la non simmetria. Supponiamo che
; da questa è evidente la non simmetria. Supponiamo che ![]() e
e ![]() .
.
Valutiamo, allora, le probabilità delle uscite applicando il teorema della probabilità totale:
![]() quindi
quindi ![]() e
e ![]() , ponendo
, ponendo ![]() .
.
Ricordiamo che ![]() ,
, ![]() ed anche
ed anche ![]() , ora
, ora 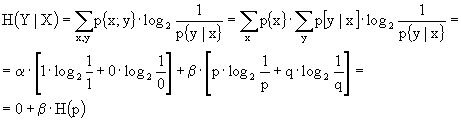
Sostituendo otteniamo ![]() .
.
Per trovare la capacità devo massimizzare I(X;Y) su una sola variabile (b). Ricordiamo che, essendo la funzione entropia simmetrica, H(p) = H(q). Inoltre è facile ricavare un'espressione semplice per la derivata dell'entropia quando questa sia espressa .in nat. Infatti ![]() .
.
Derivando H(x) in x otteniamo, ricordando che ![]() ,
,
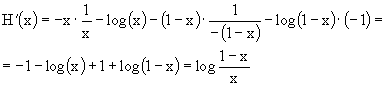
Con queste premesse, e ricordando che
![]()
eguagliando la derivata a 0, otteniamo:
![]()
sostituendo otteniamo:

Calcolo ora il valore negli estremi 0 ed 1, sostituendo questi valori a
b:![]()
Essendo uguali i valori, per il Teorema di Rolle, esiste, nell'intervallo fra 0 ed 1, sicuramente un punto in cui la derivata si annulla. Questo punto sarà, per la positività della funzione, un massimo.
Sostituendo il valore calcolato di
b nell'espressione di C, troviamo la capacità: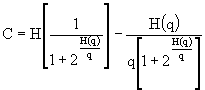 .
.
Essendo H(q) = H(p), otteniamo:
![]()
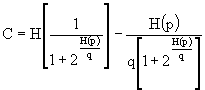 .
.
Analizziamo ora i canali continui.
I canali fisici, in natura, sono continui. Per canale fisico vogliamo, qui, intendere la porzione del canale di comunicazione che giace fra il modulatore ed il demodulatore. In questo tratto di canale i segnali di ingresso sono funzioni continue del tempo e lo scopo del canale è quello di produrre, alla sua uscita, il segnale elettrico presentatogli in ingresso. Un canale reale è descritto solo approssimativamente in questi termini. Innanzitutto, il canale modifica la forma d'onda del segnale in ingresso in modo deterministico e questo effetto può essere modellizzato adeguatamente trattando il canale come sistema lineare. Inoltre il canale modifica la forma d'onda del segnale di ingresso in modo casuale e ciò è dovuto al rumore additivo e moltiplicativo. Il rumore additivo, che può essere gaussiano o impulsivo, è più frequente di quello moltiplicativo. Il rumore gaussiano include il rumore termico ed il rumore shot. Secondo il teorema del limite centrale, il rumore risultante dalla somma degli effetti di molte sorgenti tende ad avere distribuzione gaussiana con valor medio nullo e varianza unitaria. A causa di questa "onnipresenza", il rumore gaussiano è spesso usato per caratterizzare la porzione analogica dei canali di comunicazione. Le tecniche di modulazione e demodulazione sono così scelte principalmente allo scopo di ridurre gli effetti del rumore gaussiano.
Un secondo tipo di rumore, quello impulsivo, è caratterizzato da lunghi intervalli di quiete, seguiti da scrosci di impulsi di una certa ampiezza. Questo tipo di rumore è dovuto, prevalentemente, a transitori. La sua caratterizzazione è più complessa rispetto a quella del rumore gaussiano. Inoltre le tecniche di modulazione analogica non sono così adatte, come i metodi di codifica numerica, per trattare fenomeni di rumore impulsivo. Per questi motivi gli effetti di questo tipo di rumore sono spesso impulsi nella modellizzazione della parte discreta del canale, tenendo conto, nella modellizzazione della parte analogica, del solo rumore gaussiano.
Il tipico canale continuo, secondo Shannon, è un canale di tipo additivo:
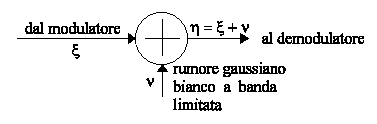
l'ingresso del canale è un processo casuale ![]() che consiste nell'insieme di tutte le forme d'onda generate dal modulatore. A questo si somma il rumore
che consiste nell'insieme di tutte le forme d'onda generate dal modulatore. A questo si somma il rumore
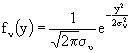 . Con questa modellizzazione stiamo, così, supponendo che le ampiezze siano infinite ma, in questi tipi di distribuzione, l'infinito è raggiunto dopo 4 o 5 s.
. Con questa modellizzazione stiamo, così, supponendo che le ampiezze siano infinite ma, in questi tipi di distribuzione, l'infinito è raggiunto dopo 4 o 5 s.
Per inciso, con questa modellizzazione non teniamo conto del fading, in quanto questo effetto è un rumore di tipo moltiplicativo.
I canali continui, quindi, hanno densità e non distribuzione di probabilità, ![]() e gli alfabeti X ed Y hanno dominio nel piano.
e gli alfabeti X ed Y hanno dominio nel piano.
Nel prosieguo si supporrà che il dominio in cui variano le variabili sia un rettangolo caratterizzato dalle rette di equazione x=a, x=b, y=c, y=d. Questo rettangolo potrà anche essere scritto, con notazione equivalente,
Q=[a,b]x[c,d]. Inoltre si ipotizzerà che la funzione densità di probabilità fxh(x,y) sia continua in Q.Il problema che ci poniamo è di sapere quanta informazione
h dia su x. La risposta, relativamente ad una trasmissione ideale, è "infinita".In realtà, Shannon dimostra che, in questo caso, la capacità del canale è finita, quindi l'informazione è finita (in quanto tutto è approssimato) e, quindi, posso trasmettere solo parte dell'informazione.
Vogliamo, ora, dimostrare che la quantità di informazione che si scambiano due variabili casuali continue è finita.

Costruiamo una sequenza di variabili casuali discrete che tendono, al limite, alle variabili casuali continue. Per far ciò divido l'intervallo [a b] in M parti e [c d] in N, suddividendo, così, il rettangolo in tanti sottorettangoli
Qij.Chiamiamo xM e hN le variabili individuate da xi ed yj.
Caratterizziamo xM e hN tramite la probabilità che assumano valori finiti, cioè
![]()
da leggersi come la probabilità che la coppia (
x,h) cada, quindi appartenga, nel rettangolo Qij. Per cui, per la probabilità degli eventi,![]() applicando il Teorema della media,
applicando il Teorema della media,
![]() in cui mis (Qij) indica l'area del rettangolo.
in cui mis (Qij) indica l'area del rettangolo.
Ora, per definizione di densità di probabilità congiunta, posso, da questa, calcolare le probabilità marginali
![]() e
e ![]()
![]()
posso, a questo punto, conoscere la probabilità che xM = xi:
![]() .
.
La stessa procedura può essere utilizzata per il calcolo di hN:
![]() .
.
Le misure di ai e bj forniscono mis (Qij) = mis (ai) · mis(bj).
Ricordando, ora, che se M ed N tendono all'infinito, allora gli intervallini diventano piccoli e xM tende a x così come hN tende a h, posso calcolare l'informazione mutua:
![]() essendo I(xM;hN) data da:
essendo I(xM;hN) data da:
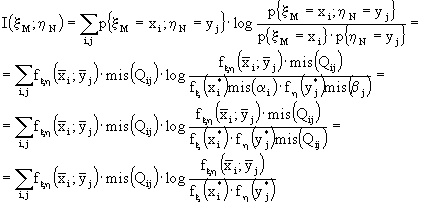
Ricordando che, al limite, la sommatoria doppia tende all'integrale doppio della funzione, dirò che:
![]()
espressione che, come per l'entropia, è una mutua informazione differenziale, in quanto la quantità è sempre positiva perché, essendo normalmente finito l'integrale e trattando con funzioni continue, l'integrale stesso converge. Quindi l'espressione stessa è proprio la mutua informazione.
Riprendiamo l'espressione dell'entropia differenziale
![]()
e riscriviamo la mutua informazione tramite l'entropia differenziale:
![]()
che è la stessa formula ricavata per le variabili casuali discrete, in cui al posto dell'entropia abbiamo sostituito le entropie differenziali.
Vogliamo, ora, dimostrare che la mutua informazione è sempre positiva o, al limite, nulla.
Esistono almeno due vie: la prima si basa banalmente sulla considerazione che ![]() in quanto è la somma di quantità positive; la seconda è più rigorosa:
in quanto è la somma di quantità positive; la seconda è più rigorosa:
se ![]() allora
allora ![]() ma
ma

Ricordando che log(x)
£ x - 1, allora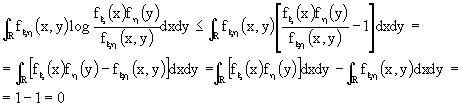
essendo densità di probabilità. Abbiamo così dimostrato che ![]() , ovvero che
, ovvero che ![]() .
.
In termini di entropia differenziale, per studiare il canale additivo è utile scrivere la mutua informazione in modo da mettere in evidenza i condizionamenti, ricordando che il rapporto fra densità congiunta e densità marginale fornisce la densità condizionata, quindi

Con procedimento analogo, si ricava il duale:
![]()
Vogliamo, ora, cercare il massimo di ![]() su tutte le densità di probabilità, quindi sulle
su tutte le densità di probabilità, quindi sulle ![]() , essendo nota la densità di probabilità
, essendo nota la densità di probabilità ![]() . Le variabili, segnale e rumore, sono statisticamente indipendenti, quindi, per ipotesi,
. Le variabili, segnale e rumore, sono statisticamente indipendenti, quindi, per ipotesi,
![]() .
.
Vogliamo cercare quale, fra tutte le densità di probabilità, è quella che rende massima l'informazione.
Dobbiamo porre che la potenza debba essere finita, e, quindi, dovrà essere finita la varianza:
![]() [
[![]() con m uguale per definizione al valor medio della variabile casuale]
con m uguale per definizione al valor medio della variabile casuale]
in quanto E[x]=0, viceversa si otterrebbero infinite funzioni.
Se non ci sono altri limiti, tutte le variabili dovrebbero essere depurate del valor medio, che non porta informazione.
Si suppone, inoltre, che il rumore sia a valor medio nullo e, quindi,
![]() in quanto E[n]=0.
in quanto E[n]=0.
Ora, se la varianza è finita ed il valor medio è nullo, allora il rumore è gaussiano.
Prima di procedere è però bene richiamare alcuni concetti sui processi ergodici e stazionari.
Per semplicità di notazione, indichiamo il set di funzioni del primo ordine con una sola espressione: pV(v;t) con la proprietà che pV(v1,t1)=pV1(v1), ecc. Dando pV(v;t), la media statistica, o valor medio, di v(t) ad ogni momento t è definita come:
![]()
e ciò significa che t è considerato costante durante l'operazione di aspettazione. Quell'equazione rappresenta una media di insieme, ovverosia una media sull'insieme di forme d'onda prese fissando il tempo.
Un'altra importante media di insieme è la funzione di autocorrelazione, definita da:
![]()
Questa aspettazione congiunta differisce in tre aspetti dalla autocorrelazione dei segnali determinati. Innanzitutto abbiamo a che fare con medie di insieme piuttosto che con medie temporali, tanto che alcuni autori enfatizzano questa differenza utilizzando simboli diversi per i due differenti tipi di autocorrelazione, inoltre ![]() dipende da t1 e t2 piuttosto che dalla singola variabile
dipende da t1 e t2 piuttosto che dalla singola variabile
Ora, un processo è stazionario se le sue caratteristiche restano invariate per tutto il tempo, ovvero se qualsiasi traslazione dell'origine dell'asse dei tempi lungo l'insieme non cambia i valori delle medie d'insieme. Fra altre conseguenze della stazionarietà, segue che il valor medio deve essere indipendente dal tempo, ovvero ![]() e che la funzione di autocorrelazione deve dipendere solo dalla differenza t1 - t2, ovvero:
e che la funzione di autocorrelazione deve dipendere solo dalla differenza t1 - t2, ovvero:
![]()
Sotto queste condizioni diciamo che il processo è almeno stazionario in senso lato.
Avendo a che fare con un processo stazionario, in senso stretto o lato, definiamo ![]() e riscriviamo la funzione di autocorrelazione come:
e riscriviamo la funzione di autocorrelazione come:
![]()
Questa espressione ha forma direttamente analoga a quella di un segnale di potenza reale e deterministico. Ponendo
t = 0 si vede subito cheCome esempio, consideriamo la sinusoide a variazione casuale di fase. Questa è un processo stazionario definito da:
![]()
se ![]() , abbiamo:
, abbiamo:
![]()
Quindi, con ![]() ed n = 1, dalla definizione di valor medio,
ed n = 1, dalla definizione di valor medio,
![]()
da cui si vede che il valor medio è nullo per tutto il tempo.
Cerchiamo, ora, la funzione di autocorrelazione:
siano ![]() ed
ed ![]() , allora:
, allora:
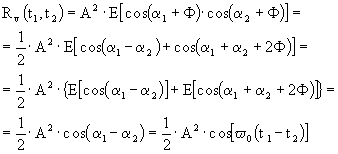
Se, ora, poniamo t1 = t2 = t, allora:
![]() . Un processo ergod
. Un processo ergod
e ciò vuol dire che il valor quadratico medio è costante nel tempo.
Se, ora, consideriamo il campione ![]() e calcoliamo la media temporale, abbiamo
e calcoliamo la media temporale, abbiamo
![]()
da cui è facile vedere che: 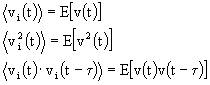
Quando tutte le medie di insieme eguagliano le corrispondenti medie temporali, il processo si dice ergodico. Un processo ergodico deve essere stazionario in senso stretto, ma la stazionarietà non garantisce l'ergodicità. L'ergodicità implica la condizione suppletiva che una singola funzione campione sia rappresentativa dell'intero processo.
Non esiste una prova semplice di ergodicità per processi arbitrari. Di conseguenza, ci accontentiamo di un approccio più pragmatico ed assumiamo un processo come ergodico se soddisfa la condizione di stazionarietà in senso lato e se, ragionevolmente, possiamo arguire che una tipica funzione campione esibisca tutte le variazioni statistiche del processo.
I processi gaussiani,- quelli, cioè, per cui valgono le seguenti relazioni:
sono ergodici e strettamente stazionari se v(t) soddisfa le condizioni per la stazionarietà in senso lato. In questo caso, possiamo stabilire le seguenti relazioni fra le medie temporali e le medie di insieme di un segnale ergodico casuale:
Alla fine di questo lungo inciso, riprendiamo la nostra trattazione continuando con le ipotesi sul segnale di ingresso: abbiamo che ![]() , quindi varianza finita e, perciò, potenza finita e
, quindi varianza finita e, perciò, potenza finita e ![]() .
.
Vogliamo calcolare la capacità del canale continuo additivo:
![]() con h = x + n
con h = x + n
ricordando che l'aspettazione di una somma è pari alla somma delle aspettazioni, calcoliamo l'aspettazione media:
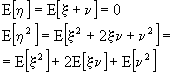
ma
x e n sono scorrelati, in quanto statisticamente indipendenti, ed a valor medio nullo, pertanto E[xn]=0 e, quindi,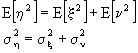 da cui
da cui
Con questi vincoli, ![]() ma
ma ![]() . Essendo x e n statisticamente indipendenti,
. Essendo x e n statisticamente indipendenti, ![]() . Dimostriamolo. Esistono diverse procedure. Vediamole:
. Dimostriamolo. Esistono diverse procedure. Vediamole:
![]()
![]() misura l'informazione assoluta trasferita per campione di y(t) a destinazione. Normalmente conosciamo la funzione densità di probabilità di transizione diretta
misura l'informazione assoluta trasferita per campione di y(t) a destinazione. Normalmente conosciamo la funzione densità di probabilità di transizione diretta ![]() piuttosto che
piuttosto che ![]() .
.
Calcoliamo allora ![]() dall'espressione equivalente:
dall'espressione equivalente:
![]()
in cui h(
h) è l'entropia della destinazione ed h(h|x) è l'entropia del rumore data da:
se il canale ha rumore additivo indipendente, così che y(t) = x(t) + n(t) allora ![]() ma
ma
![]()
dalla trasformazione lineare ![]() posso dire che:
posso dire che:
![]()
riunendo i risultati ![]() , sostituendo ottengo:
, sostituendo ottengo:
![]()
che è indipendente da f
x(x).In totale, sostituendo, otteniamo:
![]() .
.
Per altra via, fissiamo x, calcoliamo l'entropia di x + n, sapendo che sono statisticamente indipendenti; una volta calcolata quell'entropia, valutiamo la media di x + n.
Per far ciò, consideriamo la variabile z = x + y e la funzione fn(y). La prima relazione è una traslazione che si risolve in questo modo:
z = x + y; y = z - x quindi ![]() .
.
Se z = g(n) è monotona ed invertibile, è facile passare da fn(y) a fz(z); se, invece, non è monotona, bisognerà dividerla in intervalli di monotonia.
Ora, ![]() . A questo punto, posso determinare la densità di probabilità di
. A questo punto, posso determinare la densità di probabilità di ![]() e calcolare l'entropia condizionata mantenendo x fisso. In seguito, dovrò mediare su x. Siccome x e n sono statisticamente indipendenti, posso porre
e calcolare l'entropia condizionata mantenendo x fisso. In seguito, dovrò mediare su x. Siccome x e n sono statisticamente indipendenti, posso porre ![]() da cui, avendo fissato
da cui, avendo fissato ![]() , ottenere
, ottenere ![]() . Pertanto:
. Pertanto:
![]() .
.
L'intervallo di integrazione è centrato attorno ad x, quindi se n varia fra a e b, allora gli estremi sono ![]() e
e ![]() in quanto
in quanto ![]() . Se
. Se ![]() , allora
, allora ![]() .
.
Attuando il cambiamento di variabili z - x = u, allora
![]()
che è costante rispetto ad x ed è l'entropia differenziale di u. Sostituendo:
![]()
Volendo, ora, massimizzare ![]() su f
su f
Massimizzare questa quantità vuol dire che, essendo h(
n) costante ed essendoConoscendo le densità di probabilità di
h = x + n e di n, attraverso la convoluzione, conosco anche la densità di probabilità di x = h - n. Il problema si è così spostato, in quanto abbiamo effettuato il passaggio dalla ricerca delIn altri termini, dobbiamo cosiderare il massimo di:
![]() sotto i vincoli
sotto i vincoli ![]() .
.
Gli estremi sono fra ± ¥ in quanto n è gaussiano e, pertanto, definito fra ± ¥.
Per il calcolo di questo massimo, ci sono almeno due metodi analitici:
Consideriamo:
![]()
![]() .
.
Abbiamo tre vincoli, quindi dobbiamo usare tre incognite. Applichiamo la proprietà della somma degli integrali, in quanto lineari, quindi:
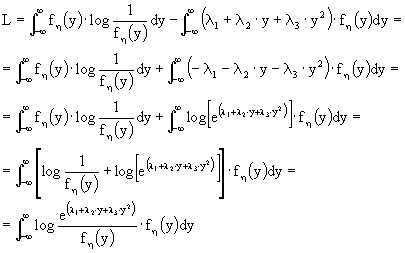
Ricordando che il log(x)
£ x - 1, abbiamo:
Questo passaggio è possibile in quanto gli integrali, ancorché generalizzati, convergono. Ricordando che ![]() otteniamo
otteniamo ![]()
Se scegliamo
l1, l2, l3 in modo che l'integrale sia una distribuzione di probabilità, diremo cheOperiamo, allora, la scelta indicata e raccogliamo le idee...
Devo massimizzare:
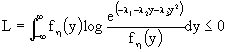
A questo punto, posso scegliere ![]() in modo tale che il limite sia raggiunto, ponendo
in modo tale che il limite sia raggiunto, ponendo ![]() . Inoltre, essendo i
. Inoltre, essendo i
La distribuzione di probabilità che massimalizza ![]() è una gaussiana, con media nulla e varianza pari a
è una gaussiana, con media nulla e varianza pari a ![]() . Quindi
. Quindi
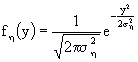
Questo metodo è rigoroso. Se avessi seguito il primo, avrei dovuto ricorrere all'equazione di Lagrange-Jacobi, valutando anche la derivata seconda, il che non è agvole.
'altro canto, avrei trovato, come limite, ![]() ed avrei dovuto porre l'ipotesi che fosse una distribuzione di tipo gaussiano, per cui
ed avrei dovuto porre l'ipotesi che fosse una distribuzione di tipo gaussiano, per cui ![]() valutando, così, dei
valutando, così, dei
Ora, se la distribuzione di probabilità della variabile
h che massimizza la mutua informazione è di tipo gaussiano e se anche, come abbiamo visto, il rumore è di tipo gaussiano, l'ingresso deve essere gaussiano, quindi
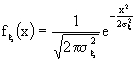
di questa variabile gaussiana,
x, voglio calcolare l'entropia: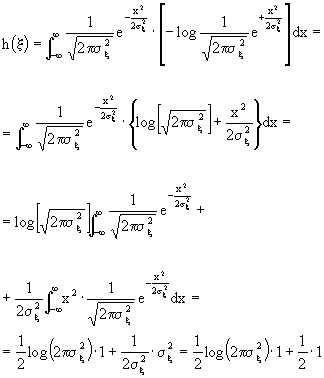
ma 1=log [e], quindi
![]() .
.
Siamo, così, pronti a calcolare la capacità di Shannon del canale additivo gaussiano bianco [Additive White Gaussian Noise = AWGN]
![]()
tenendo presente che sia f
h(y) che fn(n) sono distribuzioni gaussiane, useremo il risultato appena ottenuto, quindi: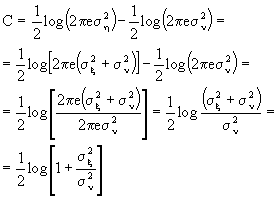
in cui ![]() è la varianza, quindi la potenza, del segnale trasmesso, mentre
è la varianza, quindi la potenza, del segnale trasmesso, mentre ![]() è la varianza, ovvero, la potenza, del rumore. Il rapporto fra queste due grandezze,
è la varianza, ovvero, la potenza, del rumore. Il rapporto fra queste due grandezze, ![]() , è il rapporto segnale rumore.
, è il rapporto segnale rumore.
Supponiamo, ora, che il canale sia strettamente limitato in banda e che la banda sia B, allora y(t) sarà un segnale completamente definito dai suoi campioni presi con frequenza di Nyquist fs = 2B. Campionare a frequenza superiore vorrebbe dire avere campioni non indipendenti e, quindi, non aggiungere nulla all’informazione.
Dualmente, potremmo supporre che segnali di ingresso e rumore siano strettamente limitati all’intervallo
(-B,B). Allora, dal teorema del campionamento, possiamo rappresentare ogni segnale usando almeno 2B campioni per secondo, ognuno avente varianza ![]() pari alla potenza P del segnale. Inoltre, abbiamo supposto che il rumore sia un processo casuale gaussiano bianco, con una densità spettrale di potenza bilatera pari a
pari alla potenza P del segnale. Inoltre, abbiamo supposto che il rumore sia un processo casuale gaussiano bianco, con una densità spettrale di potenza bilatera pari a ![]() campionata ogni
campionata ogni ![]() secondi. La sua potenza sarà quindi
secondi. La sua potenza sarà quindi ![]() . Possiamo, a questo punto, sfruttare la relazione ricavata per la capacità tenendo conto che usiamo 2B volte al secondo un canale gaussiano con capacità C data da
. Possiamo, a questo punto, sfruttare la relazione ricavata per la capacità tenendo conto che usiamo 2B volte al secondo un canale gaussiano con capacità C data da 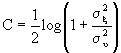 . Così, finalmente, otteniamo la capacità C di un canale gaussiano bianco limitato in banda:
. Così, finalmente, otteniamo la capacità C di un canale gaussiano bianco limitato in banda:
![]() bit/sec
bit/sec
o, se si preferisce, indicando con S/N il rapporto segnale/rumore,
![]()
Questa equazione è il Teorema (o legge) di Hartley – Shannon.
(N =
nB se la densità spettrale di potenza bilatera del rumore è n/2 W/Hz).Il teorema di Hartley – Shannon è di importanza fondamentale ed ha due importanti implicazioni.
Innanzitutto ci fornisce un limite superiore, che può essere raggiunto, per la frequenza di trasmissione di dati su un canale gaussiano. Pertanto, un progettista cercherà sempre di ottimizzare il suo sistema per avere un passo di dati il più vicino possibile a C con un tasso di errore accettabile.
La seconda implicazione del teorema di Shannon – Hartley ha a che fare con lo scambio del rapporto Segnale/Rumore con la larghezza di banda. Facciamo un esempio: supponiamo di voler trasmettere dati con la velocità di 10 Kbits/sec su un canale con banda B = 3 KHz. Per trasmettere dati alla velocità richiesta, abbiamo bisogno di un canale con capacità di almeno 10 Kbit/sec. Se la capacità del canale è minore del passo dei dati, allora non è possibile trasmettere senza errori. Così, con C = 10 Kbits/sec, dobbiamo avere un rapporto S/N pari a:
![]()
Per lo stesso problema, se avessimo avuto un canale con una banda di 10 KHz, il rapporto S/N sarebbe stato pari a 1. Perciò una riduzione della banda da 10 KHz a 3 KHz impone un aumento di potenza di 9 volte.
Un altro aspetto interessante del teorema di Shannon – Hartley è relativo alla compressione della larghezza di banda.
Proviamo a rispondere alla domanda "è possibile quantizzare e trasmettere un segnale il cui range spettrale si estende fino ad una frequenza fm su un canale con banda minore di fm?". Supponiamo di campionare un segnale analogico ad una frequenza di 3fm campioni/sec (cioè, per esempio, ad 1.5 volte la frequenza di Nyquist) e di quantizzare il valore del segnale in uno di M possibili livelli. Allora la frequenza dei dati del segnale quantizzato sarà di 3fmlog2M bits/sec. Se la banda del canale è B, allora una scelta appropriata della potenza del segnale ci consentirà di raggiungere una capacità C maggiore di 3fmlog2M. Ad esempio, con 64 livelli di quantizzazione (M=64) e con un canale di banda pari alla metà della larghezza di banda del canale, avremo bisogno di un rapporto S/N di circa 109 dB per essere in grado di trasmettere il segnale quantizzato con una piccola probabilità di errore. Perciò è possibile una compressione di banda di un fattore 2 se possiamo mantenere un rapporto S/N di 109 dB (valore impraticabile) all’uscita del canale. Assumiamo, comunque, trascurabile la distorsione del segnale dovuta al campionamento ed alla quantizzazione.
Il teorema di Shannon – Hartley ci dice anche che un canale privo di rumore ha capacità infinita. Comunque, se è presente del rumore, la capacità del cananle non si avvicina all’infinito in quanto la banda si allarga perché la potenza di rumore aumenta all’aumentare della banda.
La capacità del canale raggiunge un limite superiore finito con l’aumento della larghezza di banda se è fissata la potenza del segnale. Possiamo calcolare questo limite come segue.
Con N =
nB, in cui n/2 è la densità spettrale del rumore, abbiamo: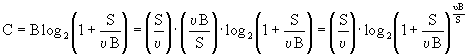
ora, ricordando che ![]() e ponendo
e ponendo ![]() , abbiamo:
, abbiamo:
![]() .
.
Un sistema di comunicazione in grado di trasmettere informazione alla velocità di Blog2(1 + S/N) è chiamato "Sistema Ideale". Shannon propose l’idea seguente per un sistema simile. Assumiamo che la sorgente emetta M messaggi equiprobabili per T secondi e che il messaggio sia codificato da un segnale di canale scelto da una collezione di M funzioni campione di rumore bianco di durata T. All’uscita del canale, il segnale ricevuto più il rumore è confrontato con le versioni immagazzinate di segnali di canale. Il segnale di canale che meglio si abbina col segnale più rumore si presume che sia stato trasmesso e, quindi, si decodifica il messaggio corrispondente. La quantità totale di ritardo necessario per osservare il segnale di messaggio, trasmetterlo e decodificarlo è, al meglio, di T secondi.
Lo schema di segnalamento ideale che utilizza segnali rumore-simili può portare informazione ad una velocità che tende alla capacità del canale solo quando T tende all’infinito. Le condizioni, quindi, sono soddisfatte solo al limite.
Sotto questa condizione limitativa, il sistema ideale ha le seguenti caratteristiche:
È ovvio che un sistema ideale non può essere realizzato in pratica. Piuttosto che cercare di progettare un sistema usando un gran numero di segnali analogici, nei sistemi pratici useremo un piccolo numero di segnali continui. Ciò implica che avremo una probabilità di errore pe non nulla. Il rate di dati e la probabilità di errore definiscono un canale discreto la cui capacità C’ sarà minore di ![]() . Tramite questo canale digitale cercheremo di raggiungere un rate di dati che si avvicina a C’ con una probabilità di errore che si avvicina a zero utilizzando codifiche digitali di controllo dell’errore. Perciò, nei sistemi pratici, cercheremo raramente di raggiungere la massima velocità teorica di trasmissione dell’informazione sulla porzione analogica del canale. Cercheremo di rendere questa parte del sistema ragionevolmente semplice. Nella parte digitale del sistema, cercheremo di raggiungere una velocità più vicina possibile alla capacità della porzione discreta del canale, in quanto la codifica digitale è più semplice da implementare.
. Tramite questo canale digitale cercheremo di raggiungere un rate di dati che si avvicina a C’ con una probabilità di errore che si avvicina a zero utilizzando codifiche digitali di controllo dell’errore. Perciò, nei sistemi pratici, cercheremo raramente di raggiungere la massima velocità teorica di trasmissione dell’informazione sulla porzione analogica del canale. Cercheremo di rendere questa parte del sistema ragionevolmente semplice. Nella parte digitale del sistema, cercheremo di raggiungere una velocità più vicina possibile alla capacità della porzione discreta del canale, in quanto la codifica digitale è più semplice da implementare.
Rima di finire questo inciso, dobbiamo sottolineare il fatto che il risultato che abbiamo ottenuto è valido per il canale gaussiano. Però questa limitazione non diminuisce l’importanza e l’utilità della legge di Shannon – Hartley in quanto: innanzitutto la maggior parte dei canali fisici sono generalmente ben approssimati dal canale gaussiano. Inoltre è stato dimostrato che il risultato ottenuto per il canale gaussiano fornisce un limite inferiore per le prestazioni di un sistema che operi su un canale non gaussiano. Cioè, se un particolare codificatore/decodificatore conduce, su un canale gaussiano, ad una probabilità di errore pe, un altro sistema di codifica/decodifica può essere progettato per un canale non gaussiano per avere una probabilità di errore minore.
Ci si è accorti del fatto che l’informazione è discreta al momento di progettare il primo sistema televisivo. Infatti, nel caso del segnale TV, bisognava stabilire sia la banda che il come trasmettere l’immagine. Il problema era diverso dalla trasmissione del canale vocale perché, in questo caso, ho un’onda di pressione da trasformare in un segnale elettrico e da riconvertire, in seguito, in onda di pressione, quindi l’onda è attesa come continua. Nel caso dell’immagine questa situazione non c’è più; infatti già col cinema si ricorre ad un sistema di discretizzazione, di campionamento. Il nostro occhio fa, poi, da filtro passa basso ricostruendo il segnale. I fotogrammi sono, di fatto, un campionamento nel sistema spazio-temporale.
Nel caso della trasmissione televisiva, si dovette ricorrere ad un secondo campionamento: un’immagine è rappresentata da una funzione in due variabili ed i sistemi di trasmissione non sono in grado di trasmettere funzioni di due variabili, quindi si doveva, in qualche modo, convertire questa funzione in un’altra ad una varabile, ovvero da F(x,y,t) (con t si tiene conto della variazione temporale) a F(x,y,nT) (con nT abbiamo il campionamento nel tempo) a f(t). Quindi si parte da una funzione di tre variabili per arrivare ad una di una. Per far ciò si utilizzarono due tipi di discretizzazione per trasmettere un segnale che è ancora continuo (solo ora, con l’HDTV si trasmette con un sistema digitale trasmettendo pixel). Una prima discretizzazione è il tempo, ma restano ancora le altre due. Bisognava, quindi, trovare una regola per passare da due variabili ad una e, questa regola, doveva essere invertibile.
Si considerò continuo il segnale (continuo) su ogni riga. Ed è continuo sia perché non si sapeva digitalizzare, che perché si riteneva che un segnale continuo trasmettesse più informazione. Considerando il segnale vocale v(t), diciamo che le frequenze presenti, quindi la F(v), vanno da 20 Hz a 20 KHz. Quindi la banda avrebbe dovuto essere di 20 KHz. In realtà bastavano 4 KHz che, di fatto, scendono ad 1.5 KHz, per trasmettere quel segnale con tutta l’informazione relativa. L’informazione contenuta nel segnale vocale era confusa con la sua caratterizzazione in frequenza. Nel caso del segnale otico, abbiamo informazioni fra i 300 ed i 700 THz e, quindi, la banda è di circa 400 THz, necessari per trasmettere non l’informazione ma il segnale stesso. Quando si è studiato il problema, ci si è accorti che 5 MHz erano sufficienti, ma si è dovuto discretizzare il segnale, sia che l’immagine fossa continua, sia che fosse fatta di punti sufficientemente piccoli.
Terminata questa discettazione sulle implicanze dei teoremi di Shannon – Hartley, torniamo al nostro sistema, composto da una sorgente e da un canale dotato di una capacità di Shannon finita. Purtroppo si utilizza il termine "capacità" anche per indicare la massima velocità, in bits/sec, con cui riusciamo a trasmettere su un doppino telefonico (100 Kbits/sec ). Questa capacità, ovviamente, non è la capacità di Shannon, che fa riferimento alla probabilità di errore. Per distinguere le due capacità, una concetto matematico e l’altra concetto fisico, la prima viene specificata come Capacità di Shannon. (Il vero limite del doppino telefonico è imposto non dalla banda, ma dal rumore: anche se noi ci basiamo sulla banda, guardiamo a monte agli errori che si commettono e definiamo, così, la tratta).
Vogliamo, ora, definire la probabilità di errore di un canale fisico, discreto, senza memoria, con capacità di Shannon C. Per poter definire la probabilità di errore, il numero degli ingressi deve essere uguale al numero delle uscite, ciò significa che l’alfabeto di ingresso e quello di uscita devono avere la stessa cardinalità: |X| = |Y|, possiamo, quindi, supporre che i due alfabeti siano uguali. Il canale è caratterizzato da una probabilità di ricezione p{y|x}. La probabilità d’errore è che trasmettendo un simbolo x se ne riceva uno diverso da x. In formule:
![]()
Gli eventi di ricevere y|x sono mutuamente esclusivi, quindi facciamo uso delle probabilità totali.
A probabilità di corretta ricezione sarà:
![]()
Se vogliamo definire la probabilità di errore e di corretta ricezione del canale dobbiamo fare riferimento alla media di tutti i simboli trasmessi:
![]()
La probabilità di corretta ricezione è:
![]()
Ci sono due relazioni che legano la capacità del canale C alla probabilità di errore pe.
La prima è costituita dal Teorema di Shannon, di cui abbiamo già parlato, che asserisce che, se la quantità di informazione di sorgente portata dal canale è minore di C, esiste una legge di codifica e di decodifica tale che la probabilità di errore, dopo la decodifica, tende a zero.
Il problema inverso è: se la quantità di informazione di sorgente è maggiore di C, allora la probabilità di errore ha un limite inferiore.
Chiamiamo con R la quantità di informazione di sorgente usata dai singoli canali. R è quindi il tasso di informazione o, come si usa dire, il rate di codifica o, anche, la velocità di codifica.
Shannon e Fano asseriscono che ![]() , relazione nota come disuguaglianza di Fano.
, relazione nota come disuguaglianza di Fano.
Se R > C, allora ![]() ed il limite è effettivo.
ed il limite è effettivo.
Se R < C, allora il limite non dice nulla in quanto non ha senso dire che ![]() .
.
Possiamo dire che la disuguaglianza di Shannon e Fano è il "converso" del Teorema di Shannon. Infatti, se uso il canale ad una velocità minore della capacità, posso avere probabilità di errore nulla, ma, senza la disuguaglianza di Fano, io non saprei cosa capita alla probabilità di errore se usassi il canale ad una velocità maggiore.
Il fatto che ![]() vuol dire che, se uso una tecnica di Shannon per annullare pe con R>C, allora, dopo la decodifica e, quindi, dopo il percorso sorgente-codifica-canale-decodificatore, la probabilità di errore tende ad 1.
vuol dire che, se uso una tecnica di Shannon per annullare pe con R>C, allora, dopo la decodifica e, quindi, dopo il percorso sorgente-codifica-canale-decodificatore, la probabilità di errore tende ad 1.
Il limite superiore del Teorema di Shannon dice che, se R<C, allora esiste un esponente di errore E® strettamente positivo tale che la probabilità di errore, dopo la decodifica, sia minore o uguale di 2 elevato al prodotto cambiato di segno dell’esponente di errore, per la lunghezza n del codice, cioè:
Se ![]()
La disuguaglianza di Shannon e Fano, discende dall’entropia condizionata H(Y|X). Essendo il limite indipendente ad X e da Y, allora l’ordine è indifferente, e potrò dire che H(Y|X)=H(X|Y).
Il teorema relativo alla disuguaglianza di Fano, dice che "dato un canale discreto senza memoria i cui alfabeti di ingresso e di uscita X ed Y abbiano la stessa cardinalità, cioè lo stesso numero N di simboli, e la cui probabilità di errore sia pe, allora è verificata la seguente disuguaglianza:
![]() "
"
Anche in questo caso, esistono diversi modi di condurre la dimostrazione. Vediamone due.

La probabilità media di errore pe è definita come:
![]()
Se le due probabilità di transizione sono uguali a p, allora il canale diventa un BSC e la probabilità di errore diventa:
![]() .
.
Generalizzando l’espressione di ![]() ad alfabeti X ed Y di cardinalità N, possiamo scrivere la possibilità media di errore come:
ad alfabeti X ed Y di cardinalità N, possiamo scrivere la possibilità media di errore come:

chiaramente, la probabilità di corretta ricezione sarà:
![]()
Definiamo l’entropia di errore H(e) come:
![]()
cioè, consideriamo H(e) come l’entropia di un alfabeto binario con probabilità pe e pc=(1-pe), che corrisponde alla quantità di informazione necessaria per specificare se un errore è occorso durante la trasmissione.
Dato questo inciso, usiamo la definizione di entropia condizionata
![]()
per scrivere:

e la definizione 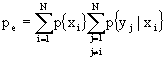 per ottenere:
per ottenere:
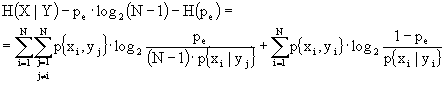 .
.
Ricordando che ![]() , otteniamo:
, otteniamo:
![]()
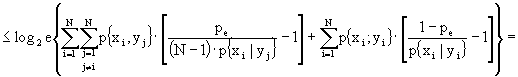
![]() (ricordando che
(ricordando che ![]() )
)
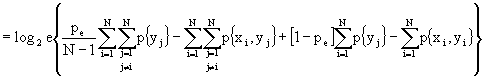
Ricordando, ora, che:
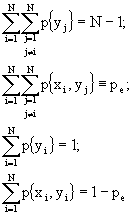
possiamo dire che:
![]()
quindi
![]()
2)
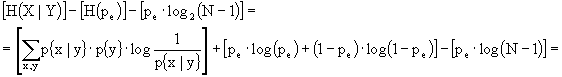
(Ricordando che la sommatoria doppia è pari alla somma di due sommatorie quando ![]() e quando
e quando ![]() )
)
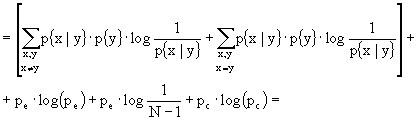
(Essendo ![]() e ricordando che
e ricordando che ![]() )
)
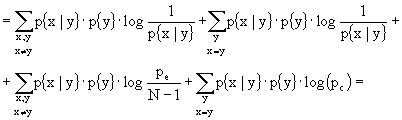
(in cui si è usato: ![]() ed in cui si è fatta la posizione che
ed in cui si è fatta la posizione che ![]() )
)
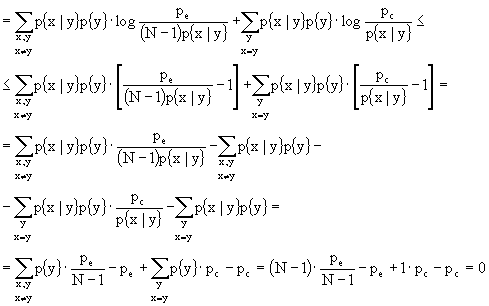
Rammentando che la capacità di un canale è maggiore o uguale alla mutua informazione, quindi
![]()
ed utilizzando il risultato appena ottenuto, cioè
![]()
che è condizione maggiore, allora ottengo, per H(X) – H(X|Y), una differenza più piccola, quindi:
![]() .
.
£
Facciamo alcune considerazioni su questi due risultati:
Il fatto che ![]() può essere visto anche in modo intuitivo. Infatti, avendo ricevuto un simbolo y
può essere visto anche in modo intuitivo. Infatti, avendo ricevuto un simbolo y
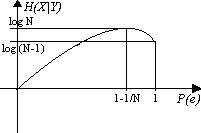
Rappresentiamo la funzione ![]() , che presenterà un massimo, in quanto somma di due curve, di cui una a campana.:
, che presenterà un massimo, in quanto somma di due curve, di cui una a campana.:
La disuguaglianza di Fano dice che le coppie di valori di H(X|Y),pe sono i punti compresi dall’area sottesa da ![]() fra i punti 0 ed 1 pari, rispettivamente, alla probabilità di errore nulla, cioè alla corretta ricezione, ed alla probabilità di errore massima, cioè 1, ovvero alla ricezione errata.
fra i punti 0 ed 1 pari, rispettivamente, alla probabilità di errore nulla, cioè alla corretta ricezione, ed alla probabilità di errore massima, cioè 1, ovvero alla ricezione errata.
Inoltre, essendo ![]() , la disuguaglianza fornisce un limite inferiore alla probabilità di errore, in termini dell’eccesso di entropia dell’alfabeto di ingresso X rispetto al flusso di informazione attraverso il canale.
, la disuguaglianza fornisce un limite inferiore alla probabilità di errore, in termini dell’eccesso di entropia dell’alfabeto di ingresso X rispetto al flusso di informazione attraverso il canale.
Considerando, ora, che I(X;Y)
£ C, possiamo dire che![]() ovvero che
ovvero che
![]()
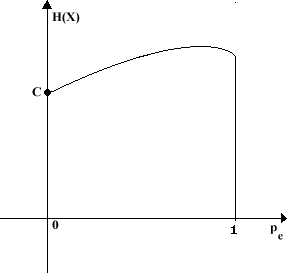
Analizzando questa curva vediamo che la regione delle coppie permesse pe;H(X) contiene punti in cui pe=0 solo se H(X)
£C. In altri termini, se l’entropia dell’alfabeto di ingresso supera la capacità del canale, allora è impossibile trasmettere informazione attraverso il canale stesso con probabilità di errore arbitrariamente piccola. Questo risultato è una versione semplificata del converso del teorema fondamentale di Shannon sulla teoria dell’informazione. Se identifichiamo l’alfabeto di ingresso del canale con l’alfabeto di uscita del codificatore di sorgente, la situazione descritta in precedenza viene a riferirsi ad un sistema di comunicazione in cui i simboli in uscita dal codificatore sono inviati direttamente lungo il canale, cioè non viene effettuata alcuna codifica. A questo punto, includiamo il codificatore di canale all’interno del nostro sistema e cerchiamo di estendere il risultato precedente. Consideriamo, così, il sistema della figura seguente:
in questa la "Sorgente" rappresenta la serie della sorgente stessa e del codificatore di sorgente. Supponiamo, per semplicità, che l’uscita della sorgente sia una sequenza di simboli binari, emessi ogni Ts secondi. Il codificatore di canale è un codificatore a blocchi, cioè trasforma blocchi di K digits consecutivi dalla sorgente (una "parola") in blocchi di n simboli appartenenti all’alfabeto X in ingresso al canale. Possiamo definire un ritmo, o rate, di codifica come ![]() .
.
Siccome dobbiamo trasmettere n simboli ogni kTs secondi, il canale deve essere usato ogni Tc = RcTs secondi. Chiamando W il set di 2k messaggi all’ingresso del codificatore di canale e con Z il set di 2k messaggi all’uscita della decodifica, possiamo applicare la disuguaglianza di Fano a questi due insiemi ottenendo
![]()
in cui il pedice W indica "Word" e la ![]() rappresenta la probabilità media di decodificare una parola d’errore, cioè una parola sbagliata. Inoltre, siccome
rappresenta la probabilità media di decodificare una parola d’errore, cioè una parola sbagliata. Inoltre, siccome ![]() ed assumendo valida la disuguaglianza
ed assumendo valida la disuguaglianza ![]() , che discende dal teorema del data processing, abbiamo:
, che discende dal teorema del data processing, abbiamo:
![]()
Siccome la trasmissione di ogni blocco di k bit implica di usare n volte il canale, possiamo dire che
![]() .
.
Sostituendo questo risultato nella formula precedente e quello che otteniamo nella disuguaglianza scritta più sopra, otteniamo:
![]() .
.
Questa disuguaglianza costituisce il converso del teorema della codifica, su cui torneremo in seguito. Siccome l’alfabeto W è costruito raggruppando k simboli consecutivi all’uscita della sorgente, l’entropia H(W) è data da:
![]()
in cui H
¥(L) è l’entropia della sorgente. Quindi la disuguaglianza vista ci dice che la probabilità di decodificare erroneamente una sequenza di k simboli non può essere resa arbitrariamente piccola quando la velocità (il ritmo) di codifica Rc è maggiore del rapporto ![]() . Dalle ultime due relazioni possiamo inferire un limite inferiore alla probabilità di errore operando come segue:
. Dalle ultime due relazioni possiamo inferire un limite inferiore alla probabilità di errore operando come segue:
![]()
Abbiamo visto che esiste un limite inferiore alla probabilità di errore, diverso da zero, quando il ritmo di codifica Rc è maggiore della capacità del canale. Vediamo ora cosa succede se Rc è minore di C. Si può provare, ed è il teorema della codifica di canale, che "Data una sorgente d’informazione binaria, con entropia pari a H
¥(L) bits/simbolo ed un canale discreto, privo di memoria, con capacità di C bits/simbolo, esiste un codice con velocità Rc=k/n per cui la probabilità di errore è limitata da:![]()
in cui E(R) è una funzione positiva decrescente, convessa su, di R per 0
£R£C". Si noti che, quando l’intera ridondanza della sorgente sia stata rimossa, H¥(L)=1, quindi R=Rc.
Basandoci sulla relazione appena vista, possiamo intraprendere tre strade per migliorare le prestazioni di un sistema di trasmissione dati:
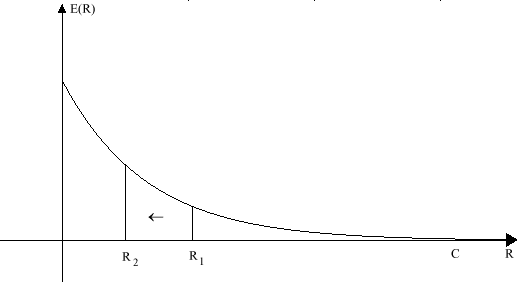
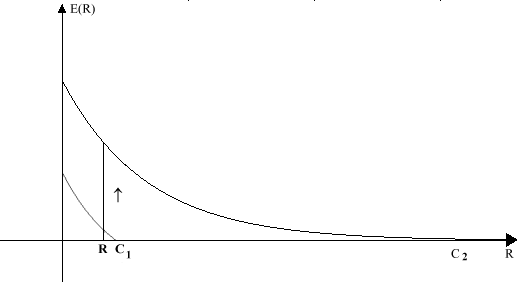
Il punto di funzionamento si sposta da E1(R) ad un maggiore E2(R), aumentando il limite d’errore.
Mentre i sistemi delineati ai punti 1. e 2. Sono rimedi ben noti per contenere i disturbi in un sistema di comunicazione, la terza strada è uno dei più grandi risultati della teoria di Shannon.